
|






 |
Автор этой задачи Ю. С. Арутюнов. Мы немного изменили условия.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ИЗ АРУТЮНОВА Ю. С.
Найти частное решение дифференциального уравнения
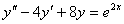 , удовлетворяющее
начальным условиям , удовлетворяющее
начальным условиям 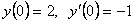 . .
РЕШЕНИЕ
Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Его общее решение представляет собой сумму общего решения соответствующего однородного уравнения и
какого либо частного решения исходного уравнения.
То есть
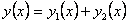 . .
Здесь 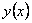 - общее решение исходного уравнения, - общее решение исходного уравнения,
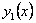 - общее решение соответствующего
однородного уравнения - общее решение соответствующего
однородного уравнения
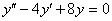 , ,
а 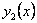 - некоторое частное решение исходного неоднородного уравнения. - некоторое частное решение исходного неоднородного уравнения.
Решим сначала соответствующее однородное уравнение
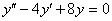 . .
Для этого решим сначала характеристическое уравнение
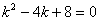 . .
Дискриминант
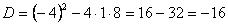 . .
Корни комплексные сопряжённые
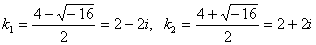 . .
Следовательно, общее решение однородного уравнения
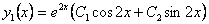 . .
В правой части исходного уравнения стоит функция 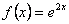 , которую можно
представить в виде , которую можно
представить в виде 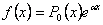 . .
Здесь 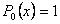 - многочлены нулевой степени (то есть попросту говоря числа). - многочлены нулевой степени (то есть попросту говоря числа).
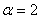 - не является корнем характеристического уравнения. - не является корнем характеристического уравнения.
Поэтому, частное решение исходного уравнения будем искать в виде
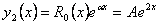
Найдём первую и вторую производные от этого решения и подставим в исходное уравнение.
Первая производная 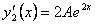 . .
Вторая производная 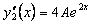
Подставляя в исходное уравнение, получим
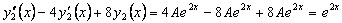 . .
Отсюда
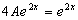 и A=0,25 . и A=0,25 .
Тогда частное решение исходного уравнения будет иметь вид 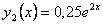 .
.
Следовательно, общее решение исходного уравнения будет иметь вид 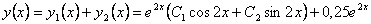 .
.
Найдём производную от общего решения 
Для определения произвольных постоянных воспользуемся начальными условиями
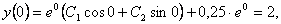 , , 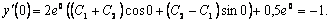 . .
Отсюда 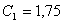 и и 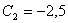 . .
Тогда частное решение, удовлетворяющее начальным условиям имеет вид 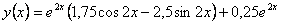 . .
Ответ: Частное решение, удовлетворяющее начальным условиям 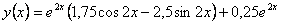 . .
Эта задача из сборника задач Арутюнова незначительно изменена.
|
|
|















