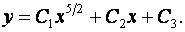Задача 10. Найти общее решение дифференциального уравнения.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
10.3. Найти общее решение дифференциального уравнения
Решение.
Это дифференциальное уравнение допускает понижение порядка, если сделать замену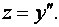 
Тогда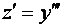 
и дифференциальное уравнение запишется в виде 
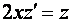или в виде
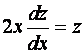
Разделим переменные в дифференциальном уравнении. Для этого умножим обе части уравнения на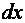 
и разделим на 
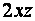Получим
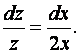
Проинтегрируем полученное дифференциальное уравнение
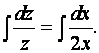
Отсюда, после взятия интегралов, получим
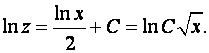
Потенциируем полученное выражение
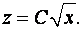
Но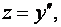 
следовательно,
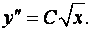
Интегрируя дважды, получим
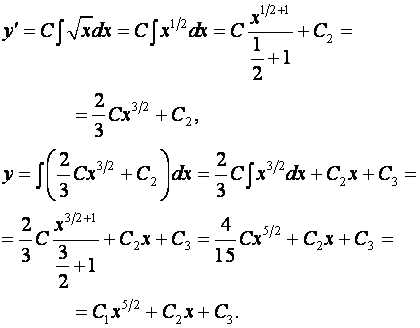
Общее решение дифференциального уравнения
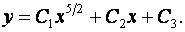
Сделаем проверку. Для этого найдём вторую и третью производные и подставим их в исходное уравнение.
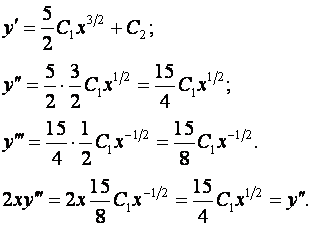
Общее решение дифференциального уравнения найдено верно.
Ответ: Общее решение дифференциального уравнения