Задача 1. Найти общий интеграл дифференциального уравнения.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
1.10. Найти общий интеграл дифференциального уравнения (Ответ представить в виде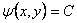 
. )
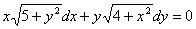
Решение.
Заданное уравнение есть дифференциальное уравнение с разделяющимися переменными. Разделим переменные. Для этого поделим обе части равенства на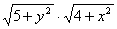 
. В результате получим
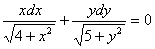.Проинтегрируем полученное дифференциальное уравнение с разделёнными переменными
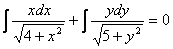. Вычислим полученные интегралы, внося
и 
под знак дифференциалов
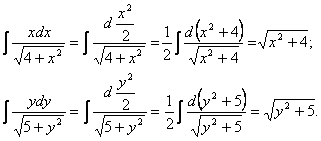.Тогда общий интеграл дифференциального уравнения запишется в виде
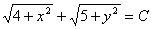.Ответ: Общий интеграл дифференциального уравнения
.
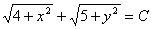