Задача 12. Найти общее решение дифференциального уравнения.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
12.17. Найти общее решение дифференциального уравнения.
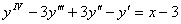.Решение.
Это неоднородное линейное дифференциальное уравнение четвёртого порядка с постоянными коэффициентами. Его решение представляется в виде
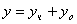. Здесь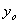 
— общее решение соответствующего однородного дифференциального уравнения
, 
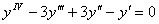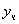— какое-либо частное решение исходного неоднородного дифференциального уравнения.
Решим сначала однородное дифференциальное уравнение
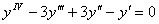.Это дифференциальное уравнение имеет характеристическое уравнение
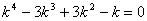.Вынося k за скобки и используя формулу для куба разности, получим
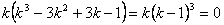. Отсюда находим корни характеристического уравнения 
.
Общее решение однородного линейного дифференциального уравнения четвёртого порядка с постоянными коэффициентами запишется в виде
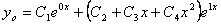
или
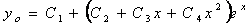. Правая часть исходного уравнения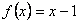 
может быть представлена в виде произведения многочлена первой степени и експоненциальной функции
. Здесь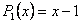 
— многочлен первой степени относительно икса; 
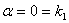— является однократным корнем характеристического уравнения.
Следовательно, частное решение может быть найдено в виде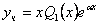 
, где 
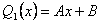— произвольный многочлен первой степени.
Таким образом,
частное решение имеет вид
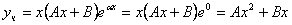.Найдём выражения первых четырёх производных для этого частного решения
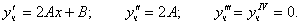. Подставим найденные выражения в исходное, неоднородное дифференциальное уравнение. Получим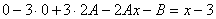 
или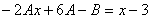 
.
Приводя подобные и приравнивая коэффициенты при одинаковых степенях, получим систему линейных алгебраических уравнений
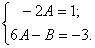.Решаем эту систему и находим
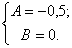. Тогда частное решение запишется
.
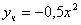Общее решение запишется
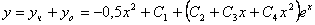.Ответ: Общее решение дифференциального уравнения
.
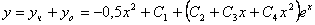