Задача 1. Построить график функции с помощью производной первого порядка.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
При решении этой задачи используется необходимое условие существования эктсремума и следующая
Теорема: Если функция, имеющая производную на отрезке, возрастает на этом отрезке, то её производная неотрицательна. Если функция непрерывна на отрезке, дифференцируема внутри отрезка, причём её производная больше нуля, то эта функция возрастает на данном отрезке.
1.3. Построить график функции с помощью производной первого порядка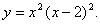 
Решение.
1) Областью определения функции является вся числовая ось. То есть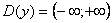 
.
2) Функция ни четная, ни нечетная, так как 
и 
.
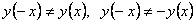3) Найдём производную функции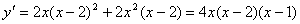 
.
4) Найдём критические точки, в которых производная обращается в ноль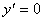 
.
Это точки 
. Отметим эти точки на числовой оси и определим знак производной на интервалах.
Таким образом: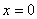 
— точка минимума; 
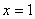— точка максимума; 
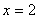— точка минимума.
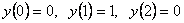. 5) Строим график на основании проделанного исследования.
.
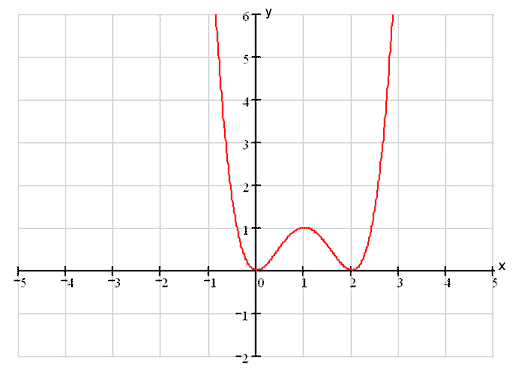