Задача 3. Найти наибольшее и наименьшее значения функции на заданном отрезке.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        3.19. Найти наибольшее и наименьшее значения функции 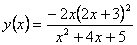        на заданном отрезке   .

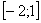Решение.

        В этой задаче используется теорема о том, что непрерывная функция достигает своего наибольшего и наименьшего значений на отрезке: либо в критических точках, где производная обращается в нуль или не существует; либо на концах отрезка. Таким образом, для того, чтобы найти наибольшее и наименьшее значения функции на данном отрезке, необходимо найти её значения в критических точках и на концах отрезка, а затем сравнить эти значения.

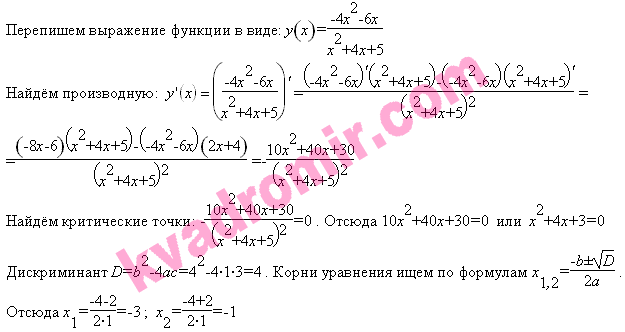
        Заданному отрезку принадлежит только точка 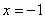  . Вычислим значения функции в найденной точке и на концах отрезка:

,     ,     _.

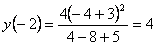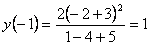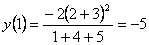        Сравнивая полученные значения, можем заключить, что наибольшее значение равно 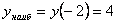  , а наименьшее значение равно   .

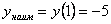        Ответ: Наибольшее значение функции на отрезке равно 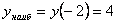  . Наименьшее значение функции на отрезке равно   .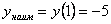