Задача 2. Вычислить определённые интегралы.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
2.5. Вычислить определённый интеграл.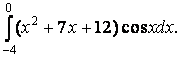 
.
Решение.
Используем формулу Ньютона-Лейбница:
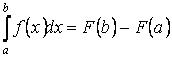
Здесь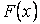 
— первообразная для функции 
.
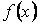Чтобы вычислить определённый интеграл применим формулу интегрирования по частям:
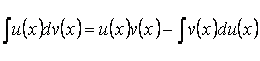
Для этого сделаем замены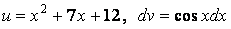 
. Тогда
.
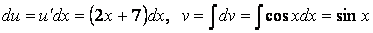Определённый интеграл запишется
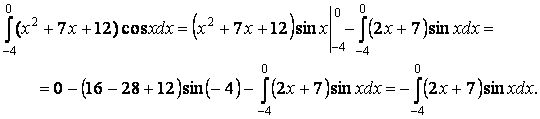
Снова применим формулу интегрирования по частям. Обозначим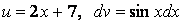 
. Тогда 
.
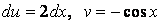Определённый интеграл запишется
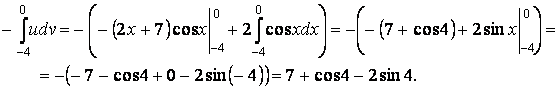
Ответ: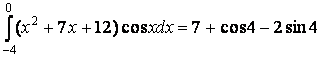 
.