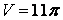Задача 20. Вычислить объёмы тел, ограниченных поверхностями.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
20.5. Вычислить объём тела, ограниченного поверхностями.
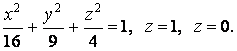
Решение.
Рассмотрим поперечное сечение  (см. рис). Тогда
(см. рис). Тогда


Поперечным сечением является эллипс с центром в начале координат. Уравнение эллипса
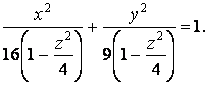
Полуоси эллипса равны
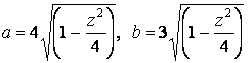
Площадь эллипса зависит от 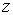 и равна
и равна
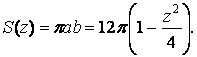 .
. При этом 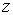 изменяется от 0 до 1. Следовательно, объем фигуры равен
изменяется от 0 до 1. Следовательно, объем фигуры равен
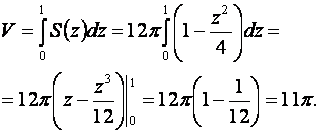
Ответ: