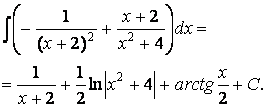
Задача 7. Найти неопределённые интегралы.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

Решение

---

        7.10. Найти неопределённый интеграл    .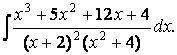

Решение.

        Чтобы найти неопределённый интеграл разложим подынтегральную дробь 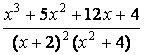    на сумму простейших дробей:

        Знаменатели исходной и полученной дробей совпадают. Следовательно, числители равны. То есть:

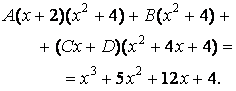
        Подставим в последнее выражение 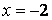. Получим или 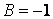. Приравниваем коэффициенты при одинаковых степенях. Получим уравнения

              

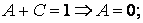
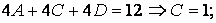
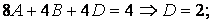
        Искомый неопределённый интеграл запишется в виде

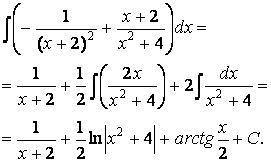
        Ответ:

---