Задача 13. Найти объем тела, заданного ограничивающими его поверхностями.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        13.6. Найти объем тела, заданного ограничивающими его поверхностями.

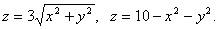
Решение.

        Перейдём к цилиндрическим координатам:

        Заданные поверхности это конус и параболоид вращения, уравнения которых в цилиндрических координатах запишутся:

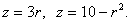
        Найдём их пересечение, решая уравнение 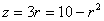  . Отсюда  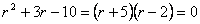   . Так как радиус положительный, то выбираем корень     .

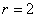        Изобразим указанное тело, и запишем его в виде неравенств

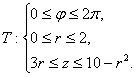
        Объём тела равен

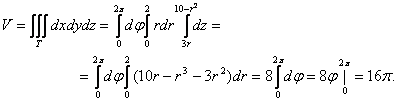
        Ответ: Объём тела равен