Задача 1. Образует ли линейное пространство заданное множество, в котором определены сумма любых двух элементов a и b и произведение любого элемента a на любое число?

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

Решение

---

        1.31. Множество всех дифференцируемых функций a=f(t), b=g(t); если сумма любых двух элементов определяется в виде 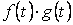, а произведение на число в виде .

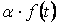Решение.

        Линейное пространство удовлетворяет нескольким аксиомама. Проверим эти аксиомы линейного пространства.
        1) Произведение двух дифференцируемых функций является дифференцируемой функцией, то есть принадлежит заданному множеству.
        2) Произведение дифференцируемой функции и некоторого числа тоже является дифференцируемой функцией.
        3)Проверим выполнение аксиом. Очевидно, что

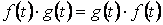    и     ,

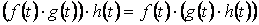        то есть первые две аксиомы выполняются.
        Единственной функцией, при умножении на которую произвольной функции последняя не изменяется, является функция 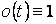. Эта функция играет роль нуля в рассматриваемом множестве.
        Функция — противоположная к данной функции 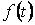, так как 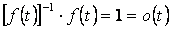. Противоположная функция определена не для каждой дифференцируемой функции, а только для тех функций, которые никогда не обращаются в нуль.
        Следовательно, рассмотренное множество не является линейным пространством.
        Ответ: Рассмотренное множество не является линейным пространством

---