
Задача 3. Найти какой-нибудь базис и определить размерность пространства решений системы.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
3.31. Найти какой-нибудь базис и определить размерность пространства решений системы.
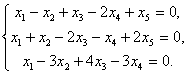
Решение.
Найдём ранг матрицы системы. Матрица системы имеет вид
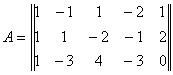 .
.Первый столбец умножим на три и прибавим к четвёртому столбцу. Первый столбец умножим на три и прибавим ко второму столбцу. Первый столбец умножим на (-4) и прибавим к третьему столбцу. Получим матрицу
 .
.Четвёртый столбец умножим на (-1) и прибавим к пятому столбцу. Второй столбец умножим на 0,5, а третий столбец умножим на 1/3. Получим матрицу
 .
.Второй столбец прибавим к третьему столбцу. Второй столбец вычтем из четвёртого столбца. Второй столбец вычтем из первого столбца. Получим матрицу
 .
.Третью строку прибавим ко второй. Первую строку умножим на (-2) и прибавим ко второй строке. Получим матрицу
 .
.Вычеркнем нулевую строку и нулевые столбцы матрицы. Получим
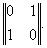 .
. Следовательно, ранг матрицы равен 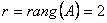 . Тогда исходная система имеет
. Тогда исходная система имеет 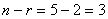 линейно независимых решений.
линейно независимых решений.
Выберем, в качестве базисных, две первые строки и два первых
столбца системы. Оставим два первых уравнения.
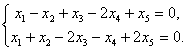 .
. Тогда переменные 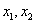 будут базисными, а остальные параметрическими. Оставим базисные переменные слева, а остальные перенесём вправо. Получим систему
будут базисными, а остальные параметрическими. Оставим базисные переменные слева, а остальные перенесём вправо. Получим систему
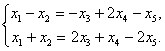 .
.Сложим оба уравнения. Из второго уравнения вычтем первое. Получим систему
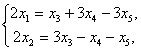
или разделив на два
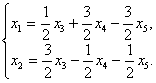 .
.Составим фундаментальную систему решений.
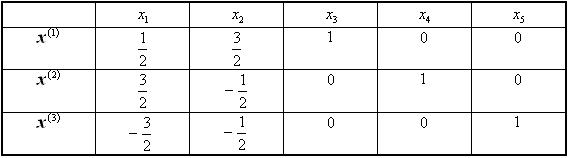
Таким образом, имеем три базисных решения
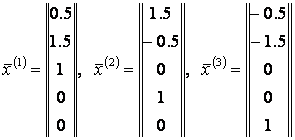 .
.Следовательно, общее решение системы уравнений
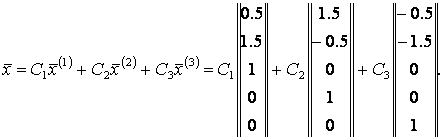 .
.