Задача 14. Найти область сходимости функционального ряда.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
Решение этого задания основано на признаке одного француза (Д’Аламбера или Коши).
Признак Д’Аламбера. Если в ряде с положительными членами
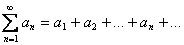
отношение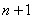 
– го члена к 
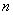– му при 
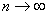имеет конечный предел 
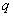, то есть
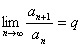, то: ряд сходится, в случае если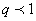 
и ряд расходится, в случае если 
.
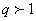Признак Коши. Если в ряде с положительными членами
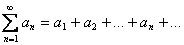
последовательность членов такова, что при 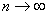существует конечный предел 
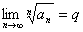, то: ряд сходится, в случае если 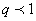и расходится, в случае если .
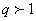Примечание: При 
оба признака бессильны и не дают ответа на вопрос о сходимости или расходимости ряда.
14.22. Найти область сходимости функционального ряда.
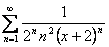
Решение.
Общий член ряда
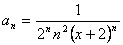. Тогда последующий член ряда получается заменой 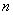на 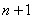. То есть
.Вычислим предел
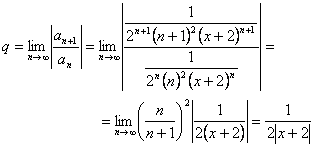. По признаку Д’Аламбера ряд сходится, если .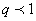
То есть, в области сходимости функционального ряда должно выполняться неравенство
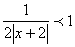.Преобразуем последнее неравенство к виду
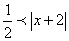
Отсюда следует, что интервал сходимости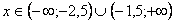 
. Исследуем сходимость ряда на концах интервала.
При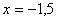 
ряд имеет вид 
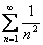. Это сходящийся ряд Дирихле.
При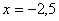 
ряд имеет вид 
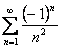. Это знакочередующийся ряд, который сходится абсолютно. Так как ряд, составленный из модулей (ряд Дирихле) сходится.
Таким образом, область сходимости исходного функционального ряда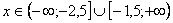 
.
Ответ: Область сходимости 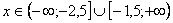.