


В фантастической литературе и кинематографе встречается описание такого сооружение, как гравитационный лифт, который представляет собой прямолинейный тоннель, проходящий сквозь толщу планеты и соединяющий две точки на её поверхности. В 2012 году наделал много шума и вызвал бурные дискуссии американский художественный фильм “Вспомнить всё”, в котором представлен такой лифт под названием “Скат”.

Дотошные знатоки, покопавшись в королевских библиотеках, установили, что впервые проект гравитационного лифта был представлен в 17 веке в письме великого Роберта Гука великом Исааку Ньютону. Технологии того времени, как и современные технологии, разумеется, не позволяли осуществить такой проект в реальности. Поэтому он и не вышел за рамки переписки двух гениев.

Много лет спустя в 1960 году немалый ажиотаж вызвала статья физика Пола Купера, опубликованная в American Journal of Physics, в которой он предложил рассмотреть проект гравитационного экспресса в качестве будущего транспортного средства. Вероятно, конгресс не выделил достаточно средств для реализации такого проекта, или для него всё ещё не созрели технологии, поскольку строительство тоннеля так и не было начато. Тем не менее, если для Земли такой проект, представляется мало возможным в ближайшей временной перспективе, так как неизбежно вызовет недовольство экологов, поскольку огромные массы породы изъятые из роющегося тоннеля придётся куда-то девать, то для нашего ближайшего спутника или для Марса этот проект может оказаться вполне подходящим способом соединения колоний расположенных по разные стороны от центра. Рассмотрим в некоторых подробностях движение гравитационного экспресса в стволе гравитационной шахты, проходящей через центр планеты.
Традиционно транспортное средство передвигающееся таким образом называют гравитационный поезд или гравитационный экспресс. Учитывая, что движении происходит по вертикали, на наш взгляд представляется более подходящим заменить термин “гравитационный поезд” термином “гравитационный лифт”. Причём в зависимости от контекста, далее под гравитационным лифтом понимается как само передвигающееся средство, так и конструкция в целом. Надеюсь, это не вызовет недоразумений.
Итак, пусть гравитационный тоннель проходит через центр планеты. В этом тоннеле под действием силы тяжести движется лифт. Первую половину пути, пока гравитационный лифт не достигнет центра планеты, он просто падает. Вторую половину пути от центра до противоположной точки на поверхности планеты гравитационный экспресс движется по инерции, которая преодолевает силу тяжести. Предполагая, что плотность вещества планеты всюду одинакова, в соответствии с теоремой Гаусса приходим к выводу, что напряжённость гравитационного поля или ускорение свободного падения \( g_* \) внутри планеты изменяется по линейному закону в зависимости от расстояния до центра планеты \( r \), а именно $$ g_* = g {r \over R} . $$Здесь \( g \) — ускорение свободного падения на поверхности планеты, \( R \) — радиус
планеты.
Считая, что гравитационный лифт не испытывает сопротивления движению, из второго закона Ньютона получим $$m g_* = m a .$$ Здесь \( m \) — масса движущегося гравитационного лифта, \( a={dv / dt } \) — его ускорение, а \( v=- dr / dt \) — скорость, которую развивает гравитационный экспресс в момент времени \( t\).
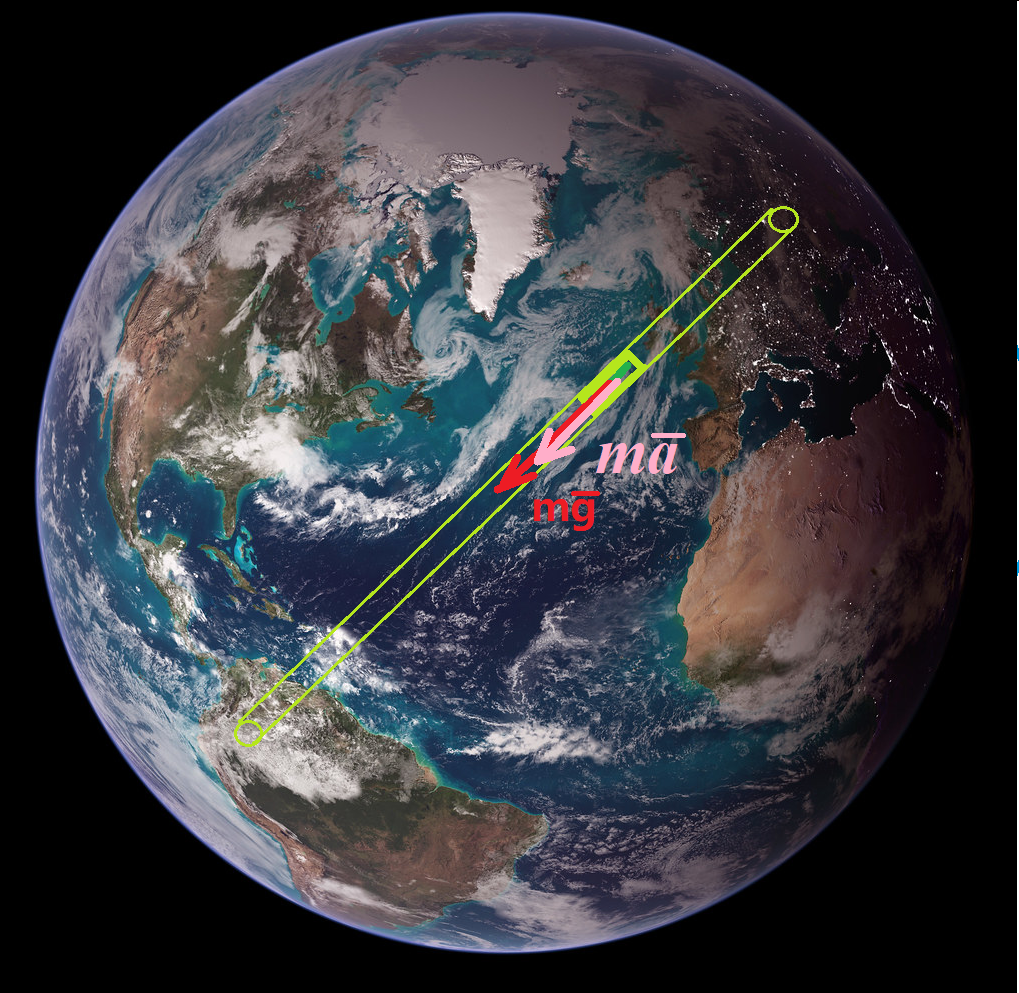
С учётом сказанного, второй закон Ньютона после сокращения массы перепишем в виде $$a = {dv \over dt} = -{ d^2 r \over d t^2 } = g {r \over R},$$ или в виде $$\ddot r + \omega^2 \cdot r = 0,$$ где \( \omega = \sqrt {g / R} \).
Общее решение полученного
дифференциального уравнения имеет вид $$r(t) = Acos\omega t +Bsin \omega t .$$ Полагая, что в начальный момент времени гравитационный экспресс покоился на верхнем этаже гравитационной шахты, то есть на поверхности планеты, приходим к начальным условиям $$r(0)=R, \qquad v(0)= \dot r(0)=0 .$$ Надо отметить, что гравитационная шахта имеет два верхних этажа, расположенных на разных концах ствола гравитационной шахты. Специфика движения гравитационного экспресса такова, что он не делает промежуточных остановок и движется без тормозов от станции отправления до конечной станции, по сути, падает с одного верхнего этажа на противоположный верхний этаж. Все промежуточные этажи являются техническими и обслуживающими работу гравитационного лифта. Между техническим этажами курсирует обычный лифт на электрической тяге, а также имеются лестничные пролёты в верхних частях гравитационной шахты. Срединная часть гравитационной шахты, в случае с Землёй, расположенная внутри твёрдого железно-никелевого ядра, а также внутри расплавленного ядра и наиболее горячей части мантии, является сверхпрочным и сверхтермоустойчивым супер-монолитом, созданным из сверх материалов, возможно, неземного инопланетного происхождения. Эта часть не обслуживается так как является одноразовой, служит в течении определённого срока, после чего заменяется на новую. Возможен вариант, когда гравитационная шахта в её сложной сверхпрочной и сверхтермоустойчивой части обслуживается специальными нанороботами камикадзе, которые следят за её состоянием и, в случае необходимости, трансформируются в жидкое состояние, заполняют собой микротрещины, возникающие в структуре супермонолита гравитационной шахты, и затем
кристаллизуются. В случае с камнем вроде Луны, центральный супермонолит шахты заменяется менее дорогостоящей конструкцией, требующей меньшего обслуживания и внимания.
Подставляя общее решение в начальные условия получим $$r(0)=Acos0+Bsin0 =A = R ,$$ $$\dot r(0) = - A \omega sin0 + B \omega cos0 = B \omega = 0 .$$
Тогда кинематическое уравнение движения запишется в виде $$r(t) = Rcos \omega t .$$ Из последнего уравнения видим, что, будучи предоставленным самому себе, гравитационный лифт совершает гармонические колебания с циклической частотой \( \omega = \sqrt { g / R } \) и амплитудой равной радиусу планеты. Период этих колебаний гравитационного лифта равен $$T = {2 \pi \over \omega } = 2 \pi \sqrt { R \over g } .$$
Гравитационный
лифт пролетает от пункта отправления до пункта назначения за время $$\tau = {T \over 2} = \pi \sqrt { R \over g } .$$ В случае с Землёй: \( g =9,8 \, м / с^2 \) , \( R = 6378 \, км \), поэтому $$\tau = 3,14 \cdot \sqrt { {6,378 \cdot 10^6} \over 9,8 } = 2533 \, c = 42 \, мин 13 \, с .$$ Для Луны: \( g =1,6 \, м / с^2 \) , \( R = 1737 \, км \), поэтому $$\tau = 3,14 \cdot \sqrt { {1,737 \cdot 10^6} \over 1,6 } = 3272 \, c = 54 \, мин 32\, с .$$ На Луне длина гравитационной шахты в разы меньше, чем на Земле, однако время движения гравитационного экспресса больше. Кажущийся парадокс объясняется тем, что Земля имеет очень горячие внутренности, чтобы не зажарится в них, нужно двигаться быстрее. С другой стороны, двигателем гравитационного лифта является сама планета, а у Земли движок помощнее, чем у Луны.

Найдём скорость экспресса $$v = - {dR \over dt} = R \omega sin \omega t .$$ В конечном пункте назначения, то есть с противоположной стороны планеты, когда \( r = - R \) и время \( t = \tau = 42 \, мин 13 \, с\), $$v = R \omega sin \omega \tau = R \omega sin \left( {2 \pi \over T} \cdot { T \over 2} \right) = R \omega sin \pi = 0 .$$ У Луны также, по мере приближения к конечной станции, гравитационный экспресс сбрасывает скорость до нуля.
Таким образом, гравитационный лифт мягко подойдёт к пункту назначения и остановится. Сцепляющее устройство зафиксирует его положение, чтобы он не начал обратное движение, после чего пассажиры покинут вагон, а службы порта начнут разгрузочно-погрузочные работы. Новые пассажиры, купившие билет на гравитационный экспресс, займут свои места. В назначенное по расписанию время, сцепляющие фиксаторы отпустят вагон. Гравитационный лифт рухнет в шахту, чтобы достигнуть пункта назначения на противоположной стороне планеты. Конечно, возможны нештатные ситуации, например, когда тектонические сдвиги деформируют ствол гравитационной шахты, или перегретая магма повредит целостность теплоизоляции. Тогда понадобится время, чтобы нанороботы камикадзе устранили поломку. При значительных повреждениях, придётся проводить более сложные ремонтные работы вплоть до замены центрального монолита и сдвига тектонических плит. Эти работы, естественно, займут время и выведут гравитационный лифт из строя на более длительный срок. В случае с Луной такие проблемы не возникнут, там даже нанороботы камикадзе не понадобятся. Так как Луна не имеет атмосферы, то и проблем с герметизацией ствола гравитационной шахты возникать не должно. Собственно, и порода, выработанная в процессе строительства гравитационной шахты, может тупо разбрасываться по поверхности Луны ровным слоем, или складываться в виде терриконов. То есть на Луне такой проект, по большому счёту, вообще не вызывает никаких проблем, кроме проблем финансирования.
Максимальную скорость вагон гравитационного лифта достигает в середине пути в центре Земли (Луны), в момент времени \( t = \tau / 2 = 21 \, мин \, 6 \, с \). Максимальная скорость гравитационного экспресса равна $$v_{max} = R \omega sin \left( {\omega \tau } \over 2 \right) = R \omega sin \left( {{2 \pi t } \over T } \cdot { T \over 4} \right) = R \omega sin \left( \pi \over 2 \right) = R \omega = R \sqrt {g \over R} = \sqrt {gR}.$$ Это первая космическая скорость. Как известно, она равна 7,9 километров в секунду. Не хило! Правда?
Для Луны первая космическая скорость значительно ниже, она равна 1,68 километров в секунду. Это лишний раз подтверждает, что строительство такого сооружения на Луне, точнее в Луне, более реалистично, а главное, более безопасно, чем его строительство в Земле.
Нет необходимости специально рассматривать случай, когда наличие каких-либо дефектов или нарушение герметизации гравитационной шахты приведёт к тому, что возникнет сопротивление движению гравитационного экспресса. Очевидно, в этом случае понадобится включение дополнительной тяги, компенсирующей возникающее трение или иное сопротивление движению. Для этой цели гравитационный лифт будет оборудован корректировочными движками и специальными датчиками, которые отслеживают возникающее сопротивление и подключают движки в том режиме, который в точности компенсирует возникшее сопротивление. К тому моменту когда наши технологии достигнут того уровня, когда мы сможем пробуравливать тоннели внутри раскалённого быстровращающегося железно-никелевого ядра нашей планеты, такие сверхточные датчики не будут представлять чего-то сверх естественного, их будут поставлять подрядчики организации, производящей и обслуживающей гравитационный лифт.
В течении всего полёта пассажиры в гравитационном экспрессе будут находиться в состоянии невесомости. Следовательно, для полёта им не понадобятся скафандры или другие средства защиты, однако, для безопасности и во избежание ушибов и травм, следует использовать ремни безопасности. Особенно это актуально в момент отправки и момент остановки экспресса, когда вес внезапно вступает в свои права.

Разумеется, в случае катастрофы, когда раскалённая магма прорвёт тоннель с движущимся лифтом или лифт застрянет в деформированном стволе шахты, тут всё, погибнут все, если не спасутся. Чтобы этого не произошло, понадобится специальная служба, которая будет следить за состоянием ядра и мантии, вроде как метеослужба в аэропорте.
Отдельно следует остановиться на правилах перевозки пассажиров в гравитационном экспрессе. Вероятно, гравикомпания, занимающаяся перевозкой пассажиров в гравитационном экспрессе, будет рекомендовать своим клиентам отказаться от употребления напитков в полёте и по возможности посетить туалет перед посадкой в гравитационный экспресс. А в самом полёте не оставлять ёмкости с жидкостью открытыми, а предметы не зафиксированными. Эти разумные требования обусловлены тем, что во время всего полёта пассажиры и все предметы внутри капсул находятся в состоянии невесомости, а в этом состоянии нет верха и низа, поэтому поведение предметов и жидкости отличны от привычного. Не то, чтобы выпить бутылочку пива или сходить в туалет было бы совсем невозможно, однако эти процедуры в невесомости сопряжены с определёнными трудностями и требуют некоторой сноровки.
Конечно, создание гравитационнго тоннеля, проходящего через центр планеты, ознаменует собой вершину гравитационного тоннелестроения и потребует огромных вложений. Вероятно, на начальном этапе развития данной технологии, будут строиться не диаметральные тоннели, а хордовые, то есть такие тоннели, которые соединяют два пункта на поверхности планеты и проходят вдоль какой-нибудь её хорды. Время движения гравитационного экспресса в таком тоннели не зависит от длины тоннеля, хотя это и покажется странным. Это время такое же, как и в сквозной диаметральной гравитационной шахте, равное 42 минуты 13 секунд, несмотря на то что преодолеваемое расстояние значительно меньше. Однако при путешествии в гравитационном экспрессе вдоль хорды пассажиры не испытывают состояния полной невесомости, а имеют уменьшенный вес, как бы являются “облегчёнными”. Причём, чем длиннее путь, тем меньше вес. Как-то так. Решение задач по физике порой преподносит нам удивительные сюрпризы.
