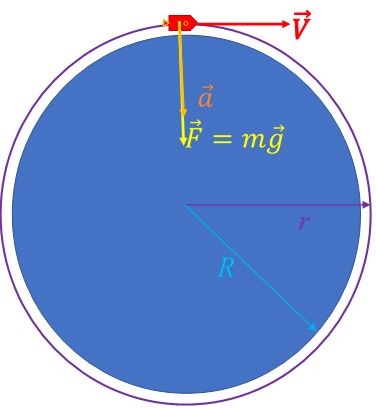
Рисунок 1.

        Камень, брошенный в горизонтальном направлении, будет летать по круговой орбите радиуса \( r=R+h\) вокруг Земли (рис. 1). По второму закону И. Ньютона$$F = {m \cdot a}.$$где \( a\) — центростремительное ускорение, равное$$a = { { V^2} \over R}. $$        Как уже было принято выше, высота \( h\) много меньше радиуса Земли \( R\) и поэтому можно считать, что радиус орбиты приблизительно равен радиусу Земли, что недалеко от истины. Таким образом,$${m \cdot a = m \cdot g } $$ и, следовательно,$$g = a = { { V^2} \over R}. $$ Из последнего уравнения выразим скорость камня$$V = \sqrt { g \cdot R}. $$ Подставив в найденное выражение значение ускорения свободного падения, которое для Земли равно \( g=9,8 { м \over с^2} \approx 10 { м \over с^2}, \) и радиус Земли \( R = 6378 км = 6,378 \cdot 10^6 м \), получим$$V = \sqrt {9,8 { м \over с^2} \cdot 6,378 \cdot 10^6 м } = 7906 \frac мс \approx 7,9 {км \over с}. $$ Это та скорость, с которой надо бросить камень или любой другой предмет, например, искусственный спутник, в горизонтальном направлении, чтобы он начал двигаться вокруг Земли по круговой орбите. Эту скорость принято называть первой космической скоростью. Мы убедились, что для Земли первая космическая скорость равна почти 8 километров в секунду.
        Согласно закону всемирного тяготения И. Ньютона, сила, с которой планета притягивает тело, равна$$F = G {M \cdot m \over r^2}. $$ Здесь \( M \) — масса планеты, \( m \) — масса тела, \( r \) — расстояние от центра планеты до тела.
Если тело находится на поверхности планеты, то расстояние от тела до её центра равно радиусу планеты \( r = R \). С другой стороны, \( F = mg \). Сравнивая два последних выражения для силы притяжения, получим выражение для ускорения свободного падения на поверхности планеты$$g = G {M \over R^2}. $$         Масса планеты равна$$M = {4 \over 3} \pi R^3 \rho , $$ где \( \rho\) — средняя плотность планеты. Подставляя выражение для массы в формулу для ускорения свободного падения, получим$$g = {4 \over 3} \pi G R \rho.$$ Тогда первая космическая скорость равна$$V = \sqrt {g \cdot R} = \sqrt {{4 \over 3} \pi G R^2 \rho } = 2R \sqrt { {\pi G \rho \over 3}}.$$То есть для планет одинаковой плотности, первая космическая скорость линейно зависит от их радиуса.

        Удивительно то, что если прорыть сквозной тоннель, проходящий через центр Земли и пустить через него лифт, то его скорость в центре Земли будет равна первой космической скорости. Такой лифт назывется гравитационный лифт или гравитационный экспресс. Решение задач по физике это очень увлекательное занятие.


        Нет сомнения, что у разных планет значение первой космической скорости будут разными, так как и радиусы планет и ускорение свободного падения на их поверхности отличаются от земных. У каждой планеты эти значения разные. Так, например, для Луны значение первой космической скорости равно \( 1,68 \) километров в секунду, так как радиус Луны равен \( 1738 \) километров, а ускорение свободного падения на Луне равно \( 1,62 \frac м{c^2} \). Значение первой космической скорости для планет солнечной системы приведены в таблице.

        Из этой таблицы видно, что пальма первенства в конкурсе первых космических скоростей, как и следовало ожидать, принадлежит Юпитеру. Однако мы забыли сказать о подлинном владыке солнечной системы — самом Солнце. Радиус Солнца \( 695500 \) километров или \( 6,955 \cdot 10^8 \) метров, а ускорение свободного падения \( 274 { м \over c^2} \). Таким образом, первая космическая скорость для Солнца равна \( 436,54 \) километра в секунду. Ясно, что ни одна планета солнечной системы не может тягаться с Солнцем по этому параметру. С другой стороны, надо быть полным идиотом, чтобы пытаться летать вокруг Солнца по близкой к нему орбите. Поэтому оставим титул чемпиона по первой космической скорости за Юпитером.
        Плутон является аутсайдером в этом состязании. Бедняга Плутон, был разжалован из числа планет в 2006 году. Многочисленные демонстрации и массовые протесты не помогли ему отстоять титул планеты, он был объявлен карликовой планетой. Карликовая планета всё равно планета, но вот только оказалось, что таких карликовых планет довольно много. В таблице ниже приведён список таких карликовых планет и значения первой космической скорости для них.

        В приведённых таблицах первая космическая скорость, а точнее её значения, весьма приблизительны ввиду дальности этих объектов и значительной неправильности их формы. В оправдание решения астрономов отказать Плутону в звании планеты следует отметить, что некоторые спутники планет, как та же Луна, превосходят его своими размерами. Но Луна не самый большой спутник в солнечной системе.

        Рассмотрим с какой угловой скоростью должна вращаться планета, чтобы её точки на экваторе двигались с первой космической скоростью. Эта угловая скорость равна$$\omega = \frac VR = \sqrt { \frac gR } = \sqrt { G {M \over R^3 }} = \sqrt { {4 \over 3 } \pi G \rho },$$где \( \rho \) — средняя плотность планеты.

        Период обращения планеты или длина суток на ней составляют$$T = { 2 \pi \over \omega } = \sqrt { {3 \pi \over {G \rho} } }.$$        Очевидно, это предельно допустимый и минимальный период обращения планеты. При меньшем периоде (большей угловой скорости) внешний слой на экваторе будет попросту отрываться от планеты. Для планеты Земля, например, \( \rho = 5515,3 {кг \over м^3}.\) Следовательно, при таком вращении сутки на Земле составляли бы$$T = \sqrt { { {3 \cdot 3,14} \over {6,67 \cdot 10^{-11} {{Н \cdot м^2} \over кг^2 } \cdot 5515,3 {кг \over м^3 } } } } = 5061,6 \ c = 84 \ мин \ 22 \ с = 1 \ час \ 24 \ мин \ 22 \ с .$$то есть в \( 17 \) раз быстрее, чем она вертится сейчас. Для Солнца этот период равен \( 10011,68 \) секунд или приблизительно \( 167 \) минут. Интересно, могут ли существовать звёзды или планеты, у которых реальный период обращения меньше рассмотренного критического значения.

        Оказывается, формула \( V = \sqrt {gR} \) возникает при решении многих других задач, которые никак не связаны с движением космических кораблей. Рассмотрим некоторые из таких задач.

        Задача. Автомобиль движется по выпуклому мосту в виде дуги окружности радиуса \( R=100 \ м.\) При какой наименьшей скорости автомобиля его колёса перестанут оказывать давление на поверхность моста и начнут отрываться от моста.

Решение

        На автомобиль, движущийся по мосту, кроме силы тяжести \( m \vec g \), направленной вниз, действует реакция опоры моста \( \vec N \), направленная вверх (рис. 2). По второму закону Ньютона$$mg-N=ma.$$Здесь центростремительное ускорение равно$$a={V^2 \over R}.$$

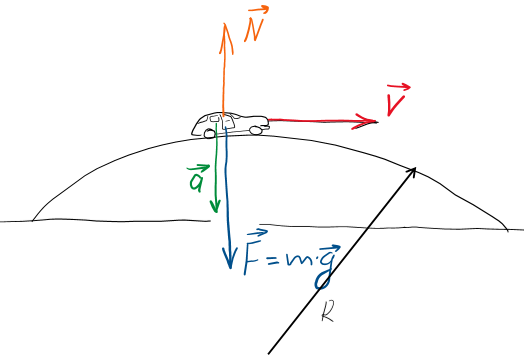
Рисунок 2.

        Однако в момент отрыва колёс автомобиля \( N = 0 \). Следовательно, \( mg = ma \) и$$g = { V^2 \over R }.$$ Откуда$$V = \sqrt { g R }.$$        Для скорости отрыва автомобиля от моста и его полёта над мостом служит та же самая формула, что и для первой космической скорости. Подставляя в эту формулу данные, получим$$V = \sqrt { { 9,8 { м \over с^2} \cdot 100 м } } = 31,3 { м \over с } \approx 113 {км \over час}.$$        Очевидно, перед въездом на такой мост должен стоять ограничитель скорости \( 110 \) километров в час или даже меньше, чтобы автомобили не прыгали, как это происходит в художественных фильмах с погоней, так называемых боевиках и триллерах.
        Ответ: \( 113 { км \over ч } \).

        Задача. В цирке бывает такой аттракцион. Из толстой металлической арматуры делается сфера радиуса \( 6 \) метров (предположительно), так что внутренность сферы достаточно хорошо просматривается зрителями, пришедшими на цирковое представление. Через специальное отверстие внутрь сферы заезжает мотоциклист на мотоцикле. Постепенно набирая скорость, мотоциклист движется по окружностям внутри сферы. Сначала эти окружности почти горизонтальные в нижней части сферы, а затем постепенно поднимаются к её экватору. В некоторый момент траектории движения мотоциклиста становятся наклонными, а затем и вертикальными. При какой минимальной скорости мотоциклиста становится возможным его движение по траектории, лежащей в вертикальной плоскости?

Решение

        Рассмотрим условия движения мотоциклиста в верхней точке траектории, когда она проходит через полюс металлической сферы (рис. 3). На мотоцикл с мотоциклистом действует сила тяжести \( m \vec g \), направленная вниз, и реакция со стороны сферической клети \( \vec N \), которая также направлена вниз. По второму закону Ньютона$$mg + N =ma \ .$$Здесь центростремительное ускорение равно$$a = {V^2 \over R } \ .$$Пока сфера оказывает давление на мотоцикл, опытный каскадёр находится в безопасности. Таким образом, допустимые значения реакции опоры определяются равенством$$N = m \cdot ( a - g ) \ge 0 \.$$

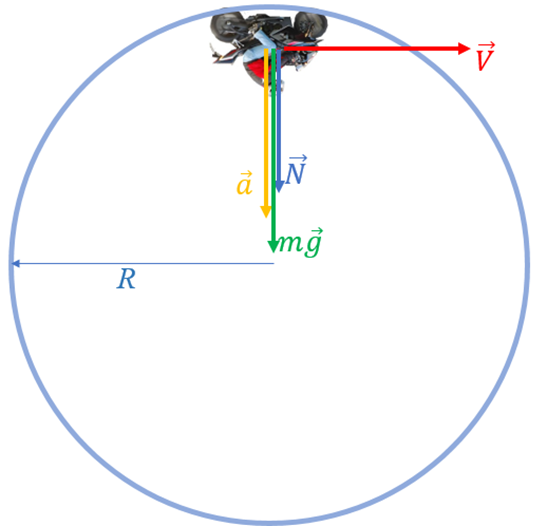
Рисунок 3.

        Проблемы у каскадёра начнутся в момент, когда \( N = 0 \). В этот момент центростремительное ускорения \( a = { V^2 \over R} \) примет значение, равное \( a = g \). Отсюда для критической скорости получаем уравнение$${ V^2 \over R} = g \ ,$$из которого находим$$V = \sqrt {gR}.$$        И опять мы видим ту же самую формулу. Минимальная критическая скорость для циркового мотоциклиста вычисляется по той же самой формуле, что и первая космическая скорость. То есть движение вокруг земной сферы подчиняется тому же критерию, что и движение внутри цирковой сферы. Законы физики, как для космонавтов, так и для цирковых каскадёров одни и те же. Подставляя в последнюю формулу данные, получим$$V = \sqrt { { 9,8 {м \over с^2} \cdot 6 м } } = 7,67 { м \over c } \approx 28 { км \over час}.$$
        Ответ: \( 28 {км \over час }.\)

        Эта скорость сравнительно небольшая. При скоростях больших \( 28 \) километров в час мотоциклисту ничего не угрожает. Главное, чтобы у него не закружилась голова. Поэтому мотоциклисту часто завязывают глаза, перед тем как он начнёт двигаться, для его же блага.


        Задача. Лётчикам асам, летающим на истребителях или спортивных самолётах, известна фигура высшего пилотажа в виде замкнутой петли, которая называется “мёртвой петлёй” или “петлёй Нестерова”. Так эту фигуру назвали в честь штабс-капитана авиации Петра Нестерова, который впервые её выполнил близ Киева 27 августа 1913 года вечером в четверть минут седьмого на самолёте французского производства “Ньюпор-4” с двигателем “Гном”. При выполнении этой фигуры самолёт движется по круговой траектории, расположенной в вертикальной плоскости. Известно, что “Ньюпор-4” с двигателем “Гном” в \( 70 \) лошадиных сил развивает скорость до \( 120 км/ч \). Пренебрегая сопротивлением воздуха, определить предполагаемый радиус “мёртвой петли” по этим данным.

Решение

        Полагая, что на самолёт в верхней точке траектории действует только сила тяжести (рис. 4), по второму закону Ньютона получим$$ma = mg.$$        При движении по окружности самолёт испытывает центростремительное ускорения$$a = {V^2 \over R }.$$

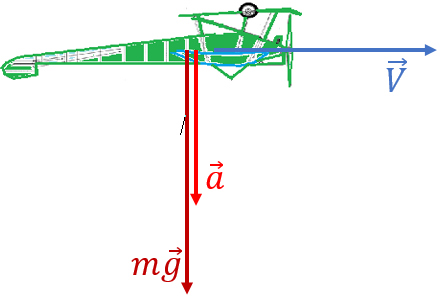
Рисунок 4.

        Из последних двух равенств находим$${ V^2 \over R} = g,$$а отсюда получаем$$V = \sqrt {gR}.$$        Снова мы видим ту же самую формулу, по которой вычисляется первая космическая скорость. То есть движение самолёта, выполняющего фигуру высшего пилотажа мёртвая петля или петля Нестерова, подчиняется тем же законам, что и движение мотоцикла в цирке, или искусственного спутника на околоземной орбите. А лётчики также подвержены действию физических законов, как и космонавты или каскадёры.
Но в задаче требуется найти не скорость, а радиус петли, так как скорость известна и равна \( 120 \) километров в час, что составляет \( 33,3 \) метра в секунду. Для радиуса получаем верхнюю оценку$$R = { V^2 \over g } = { {33,3 \frac мс}^2 \over {9,8 { м \over с^2} } } = 113,3 \frac мс.$$        Ответ:\(113,3 \, м.\)


        Задача. Ведро заполнено водой на половину. Мальчик берёт это ведро и начинает его вращать, совершая круговые движения вытянутой рукой с ведром в вертикальной плоскости так, что ведро движется по окружности радиуса около \( 1 \) метра. При этом вода не выливается из ведра. Найти скорость ведра в верхней точке траектории. С какой угловой скоростью должен мальчик вращать руку с ведром?

Решение

        Рассматривая воду как материальную точку (рис. 5), замечаем, что на неё кроме силы тяжести \( m \vec g \), направленной вниз, действует реакция дна ведра \( \vec N \), направленная тоже вниз. По второму закону Ньютона$$mg + N =ma \ .$$Здесь центростремительное ускорение$$a = {V^2 \over R }.$$        Пока \(N=m\cdot (a-g)\ge 0\) вода действует на дно, а дно на воду. Следовательно, вода не выливается из ведра. В критический момент, когда \( N = 0 \) , вода начнёт выливаться. Следовательно, если \( g \lt a \) или \( V^2 \gt gR \), вращение ведра происходит без потери воды. Отсюда для критической скорости получаем выражение$$V = \sqrt { g R }\ .$$Как видим, это точно такое же выражение, которое имеет первая космическая скорость.

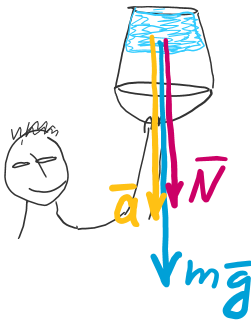
Рисунок 5.

        Подставляя в это выражение данные, получим$$V = \sqrt {9,8 { м \over с^2} \cdot 1 м} = 3,1 \frac мс \ .$$А для угловой скорости получаем$$\omega = \frac VR = 3,1 { рад \over с} \ .$$        Ответ: \( V = 3,1 \frac мс; \, \omega = 3,1 {рад \over с }.\)

        Итак, движение ведра и космического корабля, как и движение самолёта, выполняющего фигуру высшего пилотажа, и мотоцикла в цирке, подчиняются одним и тем же физическим закономерностям.


        Задача. Автомобиль, совершая поворот, движется по закруглённому участку шоссе, радиус которого равен \( 50 \) метров. Коэффициент трения колёс автомобиля об асфальт равен \( 0,4 \). Какую предельно допустимую скорость может иметь автомобиль на повороте, чтобы удержаться на трассе и не вылететь в кювет?

Решение

        При движении по закруглённому участку шоссе автомобиль удерживается на полотне благодаря силе трения между колёсами и полотном асфальта. Если бы не было силы трения или она была бы слишком маленькой, автомобиль не смог бы повернуть и проехал бы юзом слетев с трассы. Благодаря силе трения он удерживается на повороте. Применим второй закон Ньютона.$$ F_{тр}=ma.$$        Центростремительное ускорения$$a = {V^2 \over R }.$$и сила трения$$F_{тр} = \mu mg.$$где \( \mu \)— коэффициент трения.

        Подставляя во второй закон Ньютона, получим$${V^2 \over R } = \mu mg.$$Отсюда$$V = \sqrt { \mu gR }.$$        Снова мы видим ту же самую формулу, с той лишь разницей, что под корнем добавился коэффициент трения. То есть автомобиль, совершающий поворот на закруглённом участке шоссе, как и самолёт, выполняющего фигуру высшего пилотажа, как и каскадёр-мотоциклист в цирке, подобен в своём движении спутнику на околоземной орбите и подчиняется тому же закону. А водитель, получается тот же космонавт или пилот, и должен ответственно относится к данному манёвру.

        Подставляя в последнее выражение данные, получим$$V = \sqrt {0,4 \cdot 9,8 { м \over с^2} \cdot 50 м} = 14 \frac мс = 50,4 {км \over час}.$$Это предельно допустимая скорость на данном повороте. При большей скорости автомобиль будет соскальзывать с автострады. Заметим, что значение предельной скорости не зависит от массы автомобиля. Для гружённой фуры, спорткара и скутера значение предельной скорости одно и то же. Перед поворотом должен стоять знак, ограничивающий скорость в \( 50 { км \over ч } \).
        Ответ: \( 50,4 { км \over ч } \).

        Таким образом, формула, по которой определяется первая космическая скорость, является также определяющей для различных других критериальных значений скорости.

Модифицированное правило Саррюса