

1. Определитель квадратной матрицы третьего порядка. Правило Саррюса
Квадратной матрицей третьего порядка называется таблица, состоящая из трёх строк и трёх столбцов, которая обозначается в виде

Строки нумеруются сверху вниз, а столбцы слева направо. Числа, входящие в таблицу называются элементами матрицы. Первый индекс элемента указывает на номер строки, в которой он расположен. Второй индекс элемента указывает на номер столбца, в котором он расположен. Элемент aij расположен в i – ой строке и в j – ом столбце. Элементы с одинаковыми индексами a11, a22, a33 составляют главную диагональ, она расположена так, будто спускается с верхнего левого угла в нижний правый угол. На следующем рисунке главная диагональ выделена красным цветом.

Другая диагональ матрицы (определителя) содержит элементы a31, a22, a13 и называется побочной диагональю. На следующем рисунке она выделена зелёным цветом.

Определитель квадратной матрицы третьего порядка это число, обозначаемое

и равное
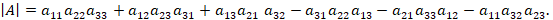 (1)
(1)Поскольку эта формула довольно сложна для запоминания, существует несколько наглядных правил или алгоритмов, позволяющих запомнить порядок действия при вычислении определителя, и, соответственно, с лёгкостью его посчитать. Одним из таких правил является правило Саррюса. Суть этого правила сводится к следующему алгоритму вычисления определителя. К матрице (определителю) приписывается справа первый и второй столбцы так, как показано на следующем рисунке.

У полученной матрицы пять столбцов. Кроме главной диагонали в полученной матрице можно мысленно выделить ещё две диагонали, параллельные главной и содержащие по три элемента. На следующем рисунке эти диагонали выделены красными отрезками.

Также можно мысленно выделить ещё две диагонали параллельные побочной и содержащие по три элемента. На следующем рисунке они выделены зелёными отрезками.

Определитель равен сумме произведений элементов, стоящих на этих шести диагоналях. При этом три произведения, соответствующие прямым, параллельным главной диагонали, надо взять со знаком плюс, а остальные три произведения, соответствующие прямым, параллельным побочной диагонали, надо взять со знаком минус.
Графически правило Саррюса можно изобразить следующим образом.
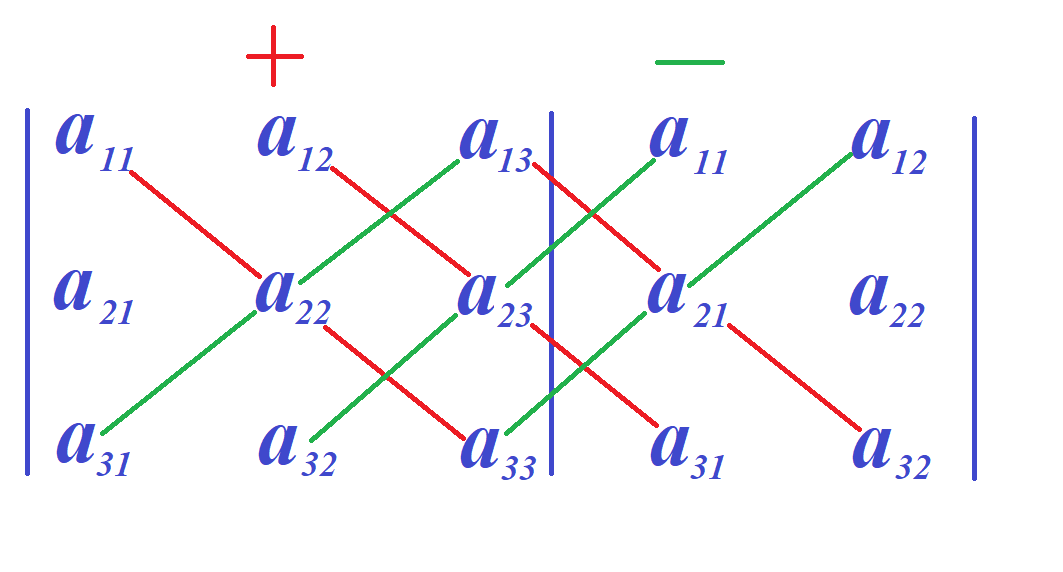
Всё, как можно видеть, довольно просто. Произведения элементов, стоящих на красных линях, складываем:

Произведения элементов, стоящих на зелёных линиях, складываем:

Затем от суммы “красных произведений” отнимаем сумму “зелёных произведений”. Получим определитель

Пример 1. Вычислить определитель

В соответствии с правилом Саррюса приписываем справа от определителя два столбца: первый (самый левый) и второй (средний) столбцы. Так, как это показано на следующем рисунке.

Складываем произведения элементов, стоящих на главной диагонали и на двух диагоналях параллельных главной, то есть произведения элементов, стоящих на красных линях, изображённых на следующем рисунке

Получим сумму

Складываем произведения элементов, стоящих на побочной диагонали и на двух диагоналях параллельных побочной, то есть произведения элементов, стоящих на зелёных линях, изображённых на следующем рисунке

Получим сумму

Тогда определитель равен

Пример 2. Вычислить определитель

Дописываем два столбца

Складываем произведение элементов, стоящих на главной диагонали и диагоналях, параллельных главной. Из полученной суммы вычитаем произведения элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на диагоналях, параллельных побочной диагонали:


2. Правило Саррюса. Столбцы слева и с двух сторон
Правило Саррюса работает и в том случае, если столбцы дописывать не справа, а слева. В этом случае слева от детерминанта дописываем третий столбец, а ещё левее второй столбец. Применяя тот же алгоритм сложения произведений диагоналей, получим искомый определитель.
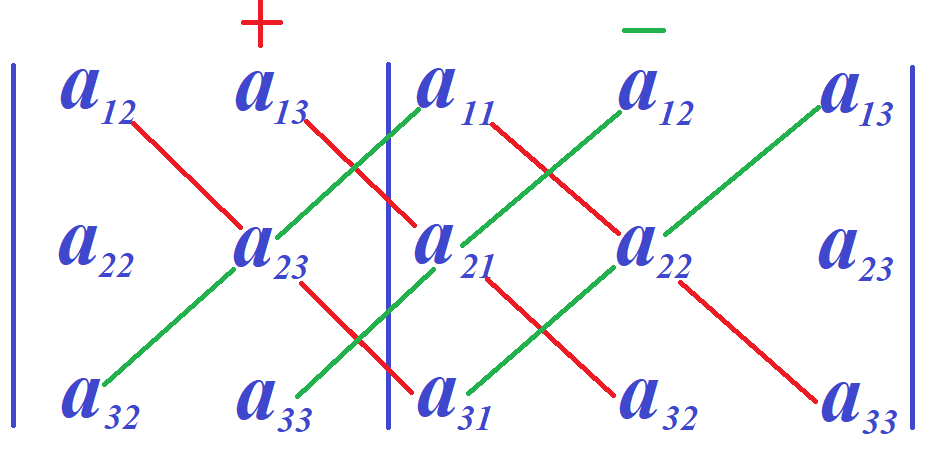
Сложим произведения элементов, стоящих на главной диагонали, и диагоналях, параллельных главной. Из полученной суммы вычтем произведения элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на диагоналях, параллельных побочной. Получим

Легко убедиться, что полученное выражение совпадает с выражением (1) из определения определителя.
Пример 3. Вычислить определитель

Допишем слева от определителя третий столбец, а затем ещё левее допишем второй столбец. От суммы произведений элементов, стоящих на красных линях, отнимем произведения элементов, стоящих на зелёных линиях.


Да, что там слева или справа, можно дописывать с обеих сторон. Именно, слева от определителя дописываем крайний правый столбец, а справа от определителя дописываем крайний левый столбец. На следующем рисунке это изображено.
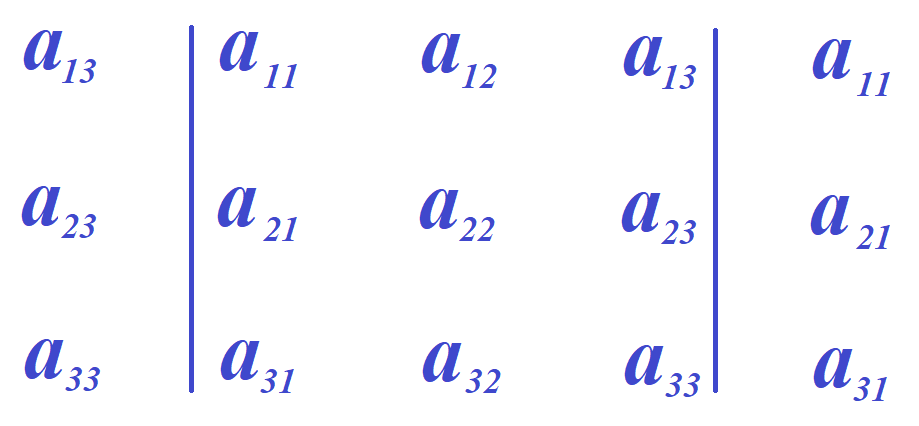
Перемножаем элементы, стоящие на главной диагонали, перемножаем элементы, стоящие на диагоналях параллельных главной. Складываем полученные произведения. От суммы отнимаем произведение элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на диагоналях, параллельных побочной.
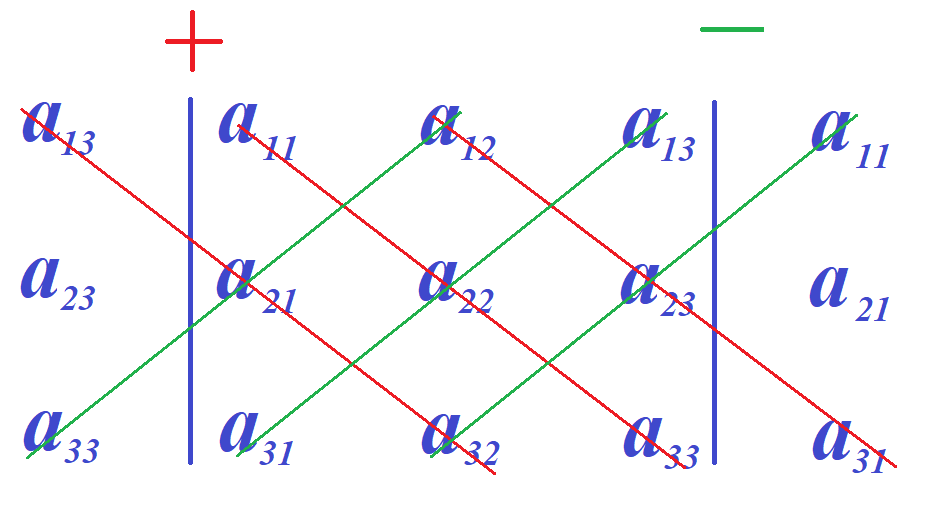
В результате этих действием получим выражение для определителя

Убедиться в том, что данное выражение равно определителю легко, если сравнить его с определением определителя (1).
Пример 4. Вычислить определитель

Допишем слева от определителя третий столбец, а справа от определителя допишем первый столбец. От суммы произведений элементов, стоящих на красных линях, отнимем произведения элементов, стоящих на зелёных линиях. Смотрите следующий рисунок.

Получим значение определителя.

3. Правило Саррюса для строк
Модификация правила Саррюса работает и в том случае, если дописывать не столбцы, а строки, например, снизу или сверху. В этом легко убедится. Действительно, подпишем снизу к определителю первую и вторую строки. Сложим произведения элементов, стоящих на главной диагонали, и диагоналях, параллельных главной. Из полученной суммы вычтем произведения элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на диагоналях, параллельных побочной, как показано на следующем рисунке.
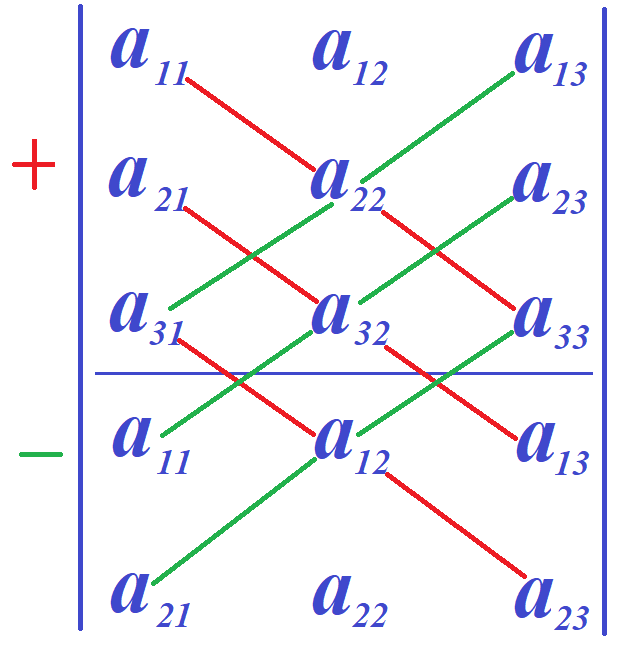
Получим

Легко убедиться, что полученное выражение совпадает с выражением (1) из определения определителя.
Пример 5. Вычислить определитель

Подпишем снизу к определителю первую и вторую строки и сложим произведения элементов, стоящих на главной диагонали, и диагоналях, параллельных главной, а из полученной суммы вычтем произведения элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на диагоналях, параллельных побочной, как показано на следующем рисунке.
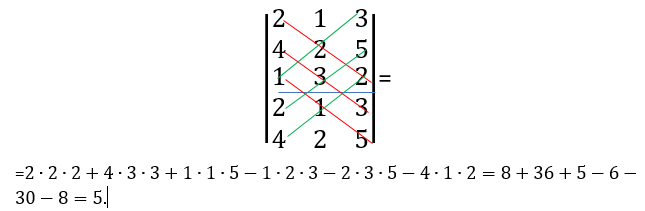
Также можно дописать строки не снизу, а сверху. Над определителем записываем самую нижнюю третью строку, а ещё выше над ней записываем вторую строку. Придерживаясь прежнего алгоритма, складывая произведения элементов, стоящих на главной диагонали и на диагоналях, параллельных главной, и вычитая из полученной суммы произвдения элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на диагоналях, параллельных побочной, получим детерминант.

Читатель может самостоятельно доказать справделивость данной разновидности правила Саррюса.
Пример 6. Вычислить определитель

Допишем сверху определителя самую нижнюю строку, а сверху неё допишем среднюю вторую строку.
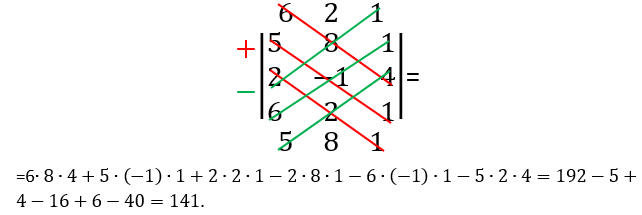
Точно, как и в случае со столбцами, строки также можно записывать и сверху, и снизу (по одной строке). Именно сверху определителя дописываем самую нижнюю строку, а снизу определителя дописываем самую верхнюю первую строку. Аналогично предыдущим случаям используем алгоритм Саррюса.
Легко проверить правило Саррюса для этого случая и убедиться, что детерминант будет найден корректно.
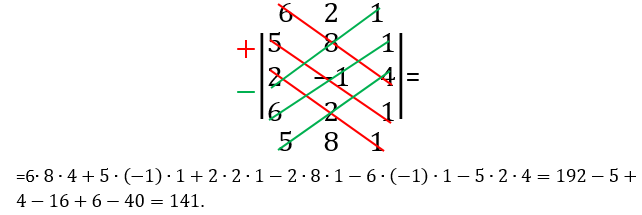
Пример 7. Вычислить определитель

Допишем сверху третью строку, а снизу первую строку. По алгоритму Саррюса, получаем значение определителя.
4. Комбинированное использование строки и столбца в правиле Саррюса
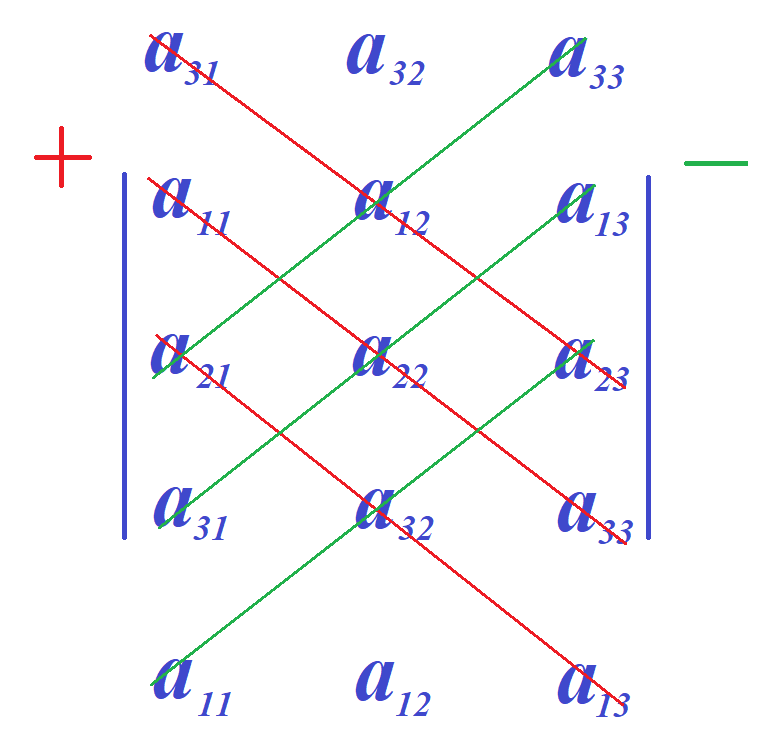
Предлагается модификация правила Саррюса, в которой дописывается и строка и столбец. Дописывается крайняя строка с противоположной стороны определителя и крайний столбец с противоположной стороны определителя. Например, допишем снизу определителя первую строку, а справа от определителя первый столбец, как на следующем рисунке.
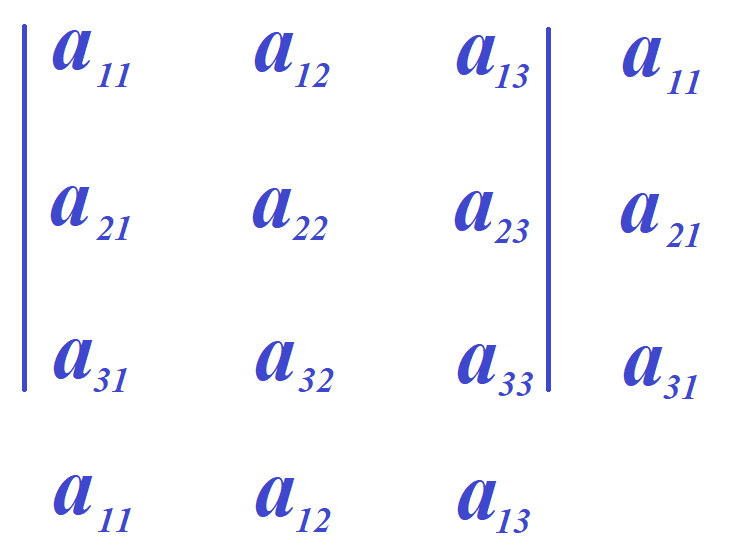
По стандартному алгоритму находим сумму произведений элементов, стоящих на главной диагонали определителя, и произведений элементов, стоящих на двух других диагоналях, параллельных главной. При этом диагональ содержит не менее трёх элементов. На следующем рисунке эти диагонали выделены красными отрезками.
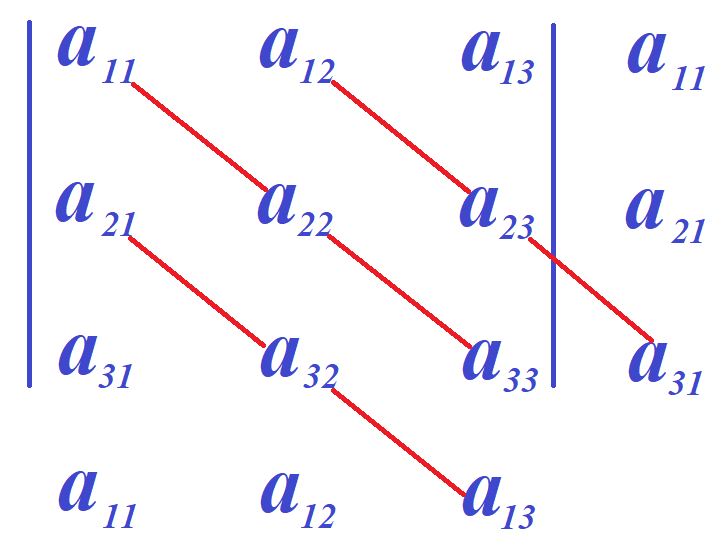
Получаем

У побочной диагонали определителя в рассматриваемой схеме, существует также две диагонали, но одна из них содержит четыре элемента a11, a32, a23 и ещё раз a11.
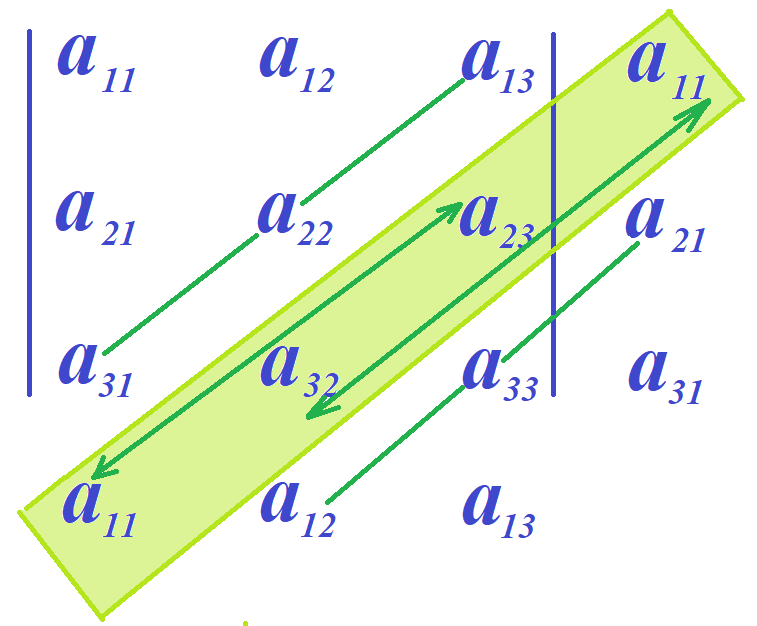
А как хорошо известно из определения детерминанта все шесть произведений, входящих в выражение определителя, должны содержать ровно три сомножителя. Поэтому в произведении, соответствующем данной диагонали, должны входить только три любых соседних по диагонали элементов: либо три нижних, либо три верхних, как это схематически указано стрелками на следующем рисунке. Благо, что оба произведения a11·a32·a23 и a32·a23·a11 одинаковы. Таким образом, для суммы произведений, соответствующих побочной диагонали и параллельных ей, получим

Разность полученных сумм равна определителю, как в этом легко убедится, сравнивая полученную разность с выражением определителя (1).

Итоговая схема может быть выбрана любой из предложенных на следующем рисунке
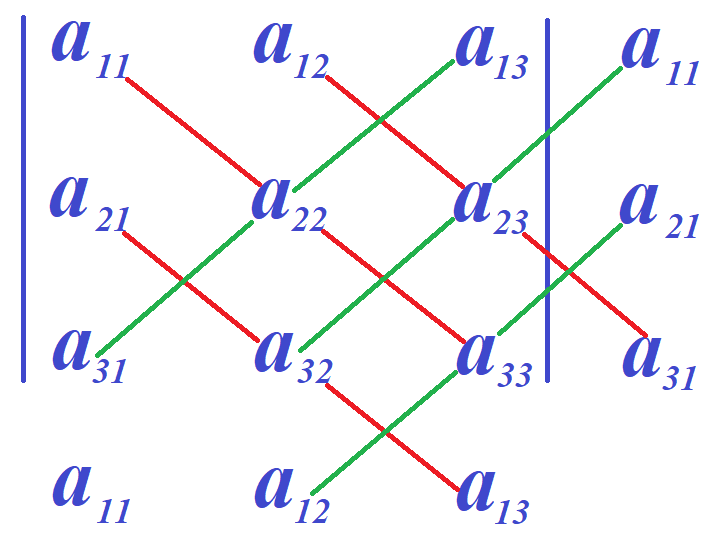

Пример 8. Вычислить определитель

Дописываем первый столбец справа от определителя, первую строку снизу под определителем.
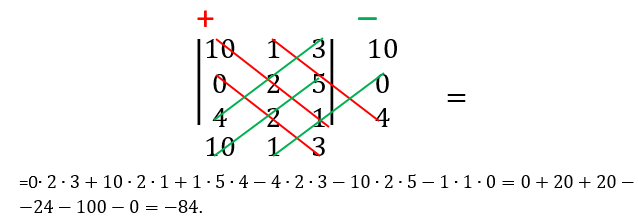
После всего сказанного, очевидно и легко проверяемо, что в алгоритме Саррюса строки и столбцы можно записывать с любой из четырёх сторон определителя. Единственное правило состоит в том, чтобы ни одна строка не соседствовала ни с одной другой дважды и ни один из столбцов не соседствовал ни с одним из других дважды. Приведём здесь лишь итоговые схемы случаев применения модифицированного правила Саррюса, оставшиеся не разобранными. Фиолетовые стрелки обозначают перенос строк (столбцов). Красные линии указывают на диагонали элементы которых перемножаются и складываются. Из полученной суммы вычитаются произведения элементов, стоящих на диагоналях, обозначенных зелёными линиями.



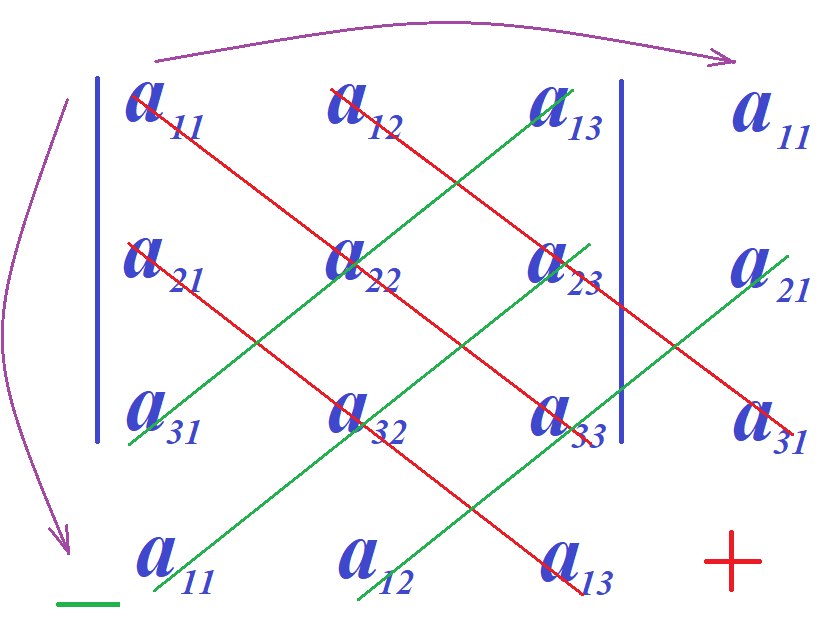

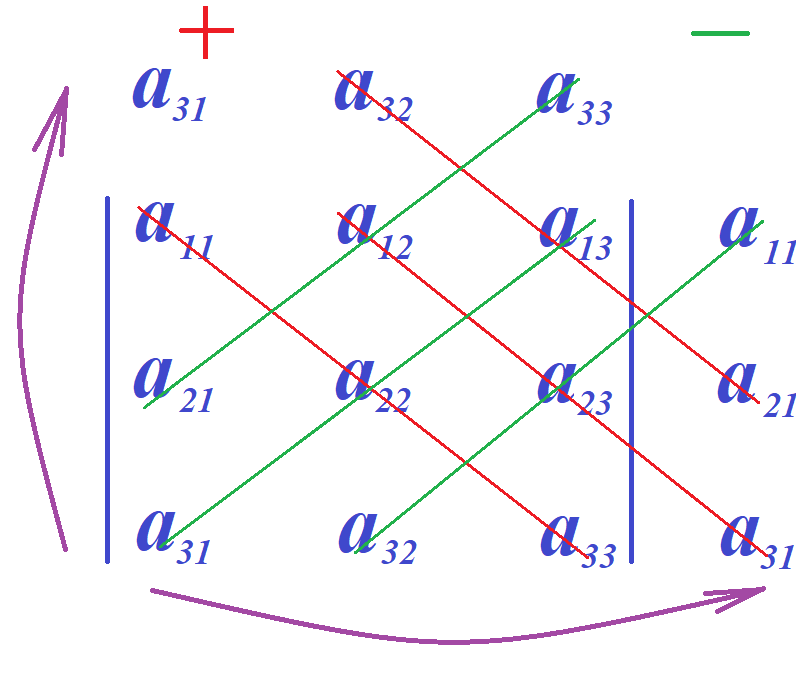

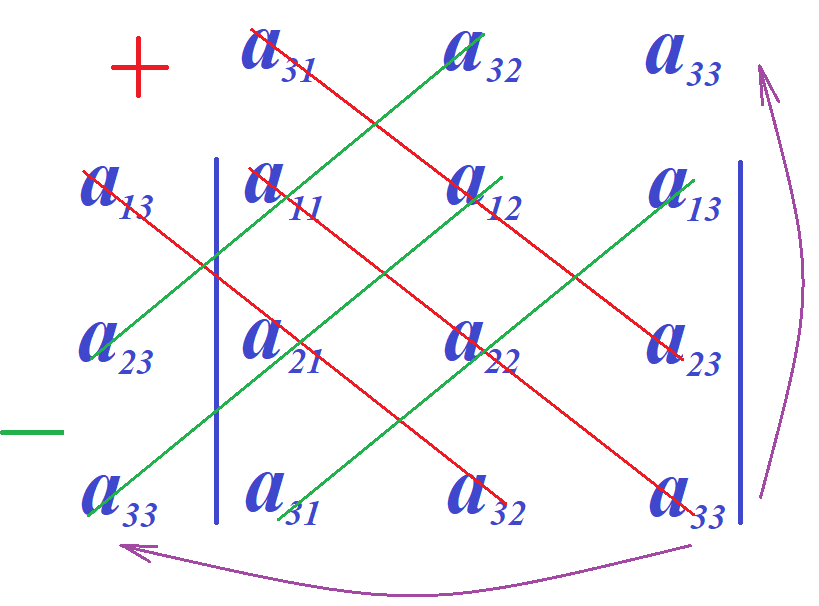
Читатель может легко убедится в корректности результатов, получаемых по этим
схемам.
5. Заключение
В заключении можем сформулировать модифицированное и обобщённое правило Саррюса следующим образом.
Если к определителю дописать пару столбцов (строк) слева или справа (снизу или сверху) так, чтобы в полученной матрице ни один столбец (строка) не соседствовал ни с одним другим столбцом дважды и не соседствовал с самим собой, то определитель равен разности между суммой произведений элементов, стоящих на диагоналях, параллельных главной диагонали, и суммой произведений элементов, стоящих на диагоналях параллельных побочной диагонали. При этом, если диагональ содержит четыре элемента, то произведение составляется из трёх любых соседних элементов, а если в диагонали менее трёх элементов, то она таковой не считается и не рассматривается.
В соответствии с модифицированным правилом Саррюса сформулируем алгоритм Саррюса.
Шаг 1.
A) Приписываются к определителю слева, или справа, или с разных сторон два различных столбца так, чтобы в полученной прямоугольной матрице ни один столбец не соседствовал дважды ни с одним другим столбцом, и не соседствовал с самим собой. То есть можно оба столбца разместить слева, оба разместить справа, или по одному столбцу с разных сторон.
или
Б) Приписываются к определителю сверху, или снизу, или и сверху, и снизу две различных строки так, чтобы в полученной прямоугольной матрице ни одна строка не соседствовала дважды ни с одной другой строкой, и не соседствовал сама с собой. То есть можно обе строки разместить сверху, обе строки разместить снизу, или по одной строке сверху и снизу.
или
В) Приписываются к определителю с любой из четырёх сторон строка и столбец так, чтобы в полученной матрице ни одна строка и ни один столбец не соседствовали дважды ни с одной другой строкой (столбцом), и не соседствовали с собой.
Шаг 2.
Перемножаются три элементы, стоящие на главной диагонали. Перемножаются отдельно элементы, стоящие на каждой из двух диагоналей, параллельных главной и содержащей три элемента. Составляется сумма из трёх произведений.
Перемножаются три элементы, стоящие на побочной диагонали. Перемножаются отдельно элементы, стоящие на каждой из двух диагоналей, параллельных побочной и содержащей три элемента. Составляется сумма из трёх произведений.
В обоих случаях, если диагональ содержит четыре элемента, то произведение составляется из трёх любых соседних элементов, а если в диагонали менее трёх элементов, то она не рассматривается.
Шаг 3.
Находится разность между первой и второй суммами, которая равна искомому определителю.
