

Таблица чисел $$A=\begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}$$ называется квадратной матрицей второго порядка. Матрица второго порядка состоит из двух строк и двух столбцов.
Определителем или детерминантом квадратной матрицы \(A\) называется число, обозначаемое \(detA\) или $$|A|=\begin{vmatrix} a & b \\ c & d \\ \end{vmatrix}$$ и равное \(ad-bc\).
Таким образом, определитель матрицы это есть
$$detA=|A|=\begin{vmatrix} a & b \\ c & d \\ \end{vmatrix}=ad-bc.$$
Например $$\begin{vmatrix} 2 & 4 \\ 1 & 3 \\ \end{vmatrix}=2\cdot 3-4\cdot 1=6-4=2,$$ или $$\begin{vmatrix} 5 & -3 \\ 4 & 3 \\ \end{vmatrix}=5\cdot 3-(-3)\cdot 4=15+12=27.$$
Очевидно, вычисление определителя матрицы второго порядка не представляет сколько-нибудь серьёзной проблемы.
Таблица чисел $$A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{pmatrix}$$ называется квадратной матрицей третьего порядка.
Числа \(a_{ij}\) называются элементами матрицы.
Матрица третьего порядка состоит из трёх строк и трёх столбцов. Первый индекс \(i\) указывает на номер строки, а второй индекс \(j\) указывает на номер столбца.
Определитель квадратной матрицы третьего порядка \(A\) это число, которое также называется детерминант матрицы, равное
$$|A|=detA=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix}=\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad $$ $$=a_{11} \cdot a_{22} \cdot a_{33} +a_{12} \cdot a_{23} \cdot a_{31}+a_{13} \cdot a_{32} \cdot a_{23}-a_{13} \cdot a_{22} \cdot a_{31}-a_{12} \cdot a_{33} \cdot a_{21}-a_{11} \cdot a_{23} \cdot a_{32}.$$
Эту формулу довольно трудно запомнить. Поэтому применяют правило, которое называется правило Саррюса. Сейчас я его опишу.
Детерминант квадратной матрицы третьего прядка \(A\) считается так.
Выписываем матрицу в прямых скобках и приписываем к ней справа первый и второй столбцы. Потом перемножаем те элементы, которые лежат на наклонных линиях. Произведения, лежащие на линиях идущих справа и сверху влево и вниз складываются. Эти линии на рисунке помечены плюсиком и нарисованы жёлтым цветом. От полученной суммы вычитают произведения, лежащие на других трёх линиях, помеченных минусиком и нарисованных голубым цветом. Смотри на рисуночек ниже.
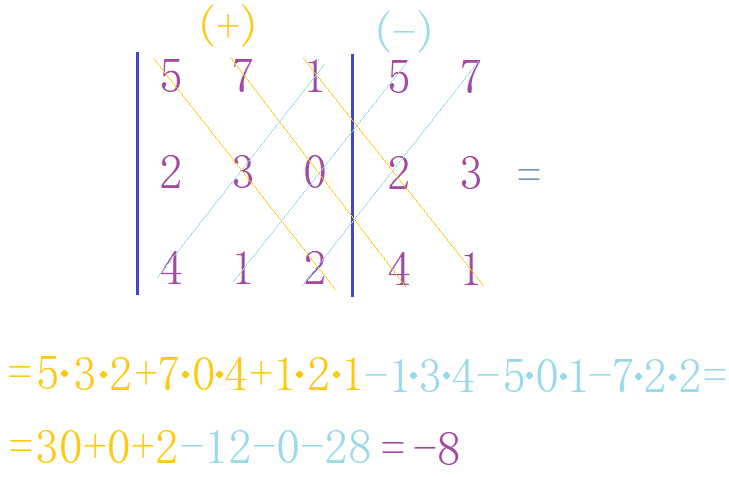
Примечание.
Есть ещё другое правило, которое называется правилом треугольников
Слагаемые в правой части равенства представляют собой произведения элементов определителя, взятых по три так, как показано на двух следующих схемах:
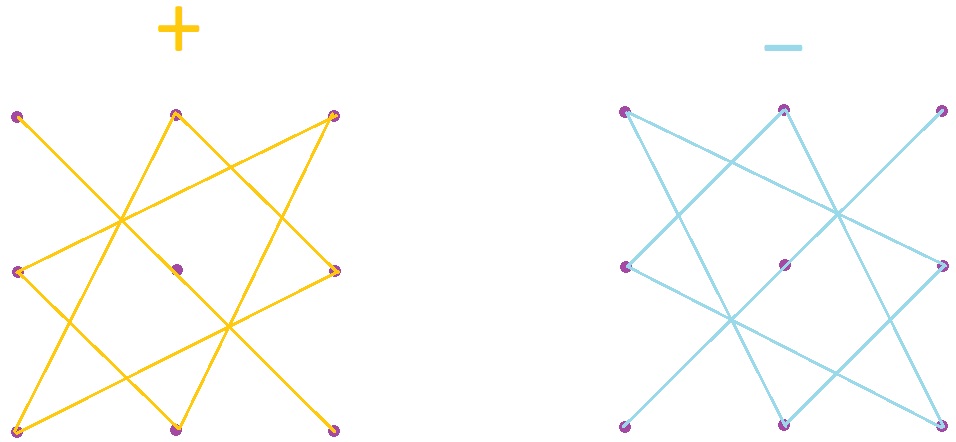
Метод детерминантов или метод Крамера
Пусть дана система уравнений с тремя неизвестными $$\left\{ \begin{array}{c} a_{11}x+a_{12}y+a_{13}z=b_1,\\ a_{21}x+a_{22}y+a_{23}z=b_2,\\ a_{31}x+a_{32}y+a_{33}z=b_3.\\ \end{array} \right. $$
Основной определитель системы — это определитель составленный из коэффициентов стоящих при неизвестных
$$\Delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix}.$$
Числа, стоящие справа от знаков равно называются свободными членами.
Первый вспомогательный определитель составляется из основного заменой первого столбика столбиком свободных членов. Вот так $$\Delta_x=\begin{vmatrix} b_1 & b_2 & b_3 \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix}.$$
Второй вспомогательный определитель составляется из основного заменой второго столбика столбиком свободных членов. Вот так
$$\Delta_y=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ b_1 & b_2 & b_3 \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix}.$$
Третий вспомогательный определитель составляется из основного заменой третьего столбика столбиком свободных членов. Вот так $$\Delta_z=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ b_1 & b_2 & b_3 \\ \end{vmatrix}.$$
Если основной определитель системы отличен от нуля \(\Delta \neq 0\), то система имеет единственное решение. Это решение находится по формулам $$x={\Delta_x \over \Delta}, \qquad y={\Delta_y \over \Delta}, \qquad z={\Delta_z \over \Delta}. \qquad $$
