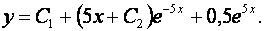Задача 15. Найти общее решение дифференциального уравнения.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        15.25. Найти общее решение дифференциального уравнения.

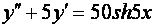
Решение.

        Дифференциальное уравнение имеет следующее характеристическое уравнение

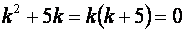
        Его корни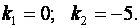  
        Cоответствующее однородное дифферренциальное уравнение

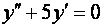
        Общее решение однородного дифференциального уравнения имеет вид

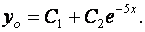
        Правая часть исходного дифференциального уравнения имеет вид

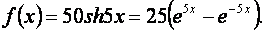
        В соответствии с этой правой частью частное решение исходного дифференциального уравнения ищем в виде

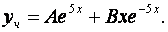
        Дифференцируем дважды это частное решение

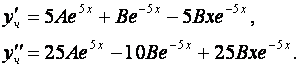
        Подставим найденные производные и функцию в исходное дифференциальное уравнение

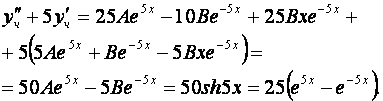
        Отсюда, получим 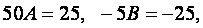или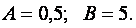

        Таким образом, исходное дифференциальное уравнение имеет следующее частное решение

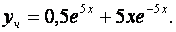
        Общее решение неоднородного линейного дифференциального уравнения представляет собой сумму какого-либо частного решения исходного уравнения и общего решения соответствующего однородного дифференциального уравнения. То есть

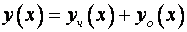
        Подставляя найденные решения, для общего решения исходного неоднородного линейного дифференциального уравнения получим

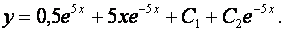
        Ответ: Общее решение дифференциального уравнения