Задача 4. Найти решение задачи Коши.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
4.7. Найти решение задачи Коши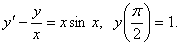 
Решение
Это линейное, неоднородное уравнение первого порядка, и для него мы сейчас найдём решение задачи Коши. Будем искать решение задачи Коши, по методу Бернулли, в виде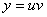 
. Тогда производная 
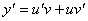. Подставим в исходное уравнение. Получим
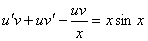.Перепишем уравнение в виде
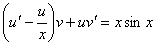
Примем, что
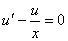
Тогда
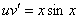.В первом уравнении разделим переменные
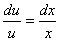
и проинтегрируем его
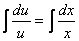
Получим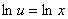 
. Отсюда 
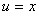. Тогда другое уравнение запишется в виде 
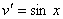. Интегрируем и его 
.
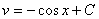Тогда, общее решение исходного дифференциального уравнения запишется
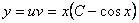. Но это ещё не решение задачи Коши. Никто и не говорил, что задача Коши решается легко.
Воспользуемся начальным условием для определения неизвестного С.
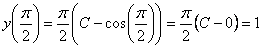
Отсюда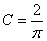 
. Тогда частное решение — решение задачи Коши — запишется
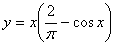
Сделаем проверку. Для этого производную найденного решения
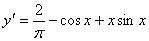
и само решение подставим в исходное уравнение и начальное условие. Уравнение обращается в тождество
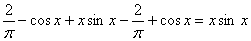.Начальное условие удовлетворяется
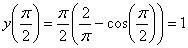. Следовательно, решение задачи Коши найдено верно.
Ответ: Решение задачи Коши
.
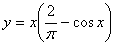