
Задача 14. Вычислить площади фигур, ограниченных графиками функций.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
14.1. Вычислить площадь фигуры, ограниченной графиками функций.  .
.
Решение.
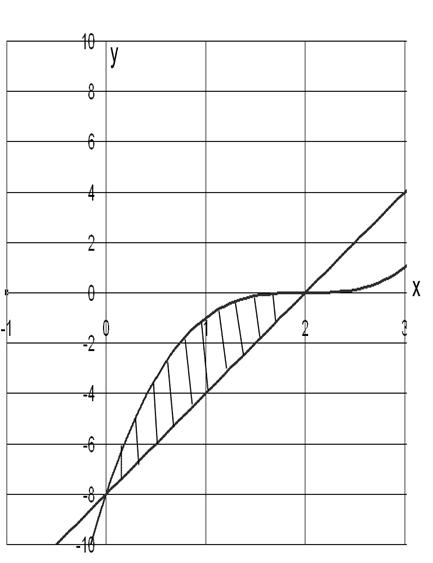
Изобразим графики функций и найдём точки их пересечения.
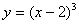 — кубическая парабола, проходящая через точку (2;0).
— кубическая парабола, проходящая через точку (2;0).
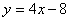 — прямая, проходящая через точки (0;-8) и (2;0).
— прямая, проходящая через точки (0;-8) и (2;0).
Пересечение графиков найдём, решая уравнение 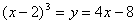 или
или 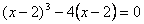 .
.
Отсюда 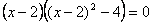 или
или 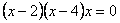 . Это уравнение имеет корни
. Это уравнение имеет корни 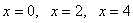 .
.
Фигура ограниченная заданными линиями состоит из двух одинаковых частей. Поэтому площади фигуры равна удвоенной площади одной части
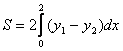
Подставляя выражения для функций, получим
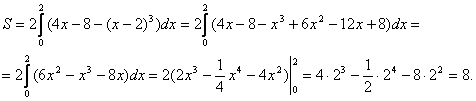
Ответ: S=8.