
Задача 15. Вычислить площади фигур, ограниченных линиями, заданными уравнениями.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
15.6. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями.
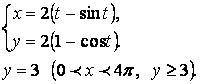
Решение.
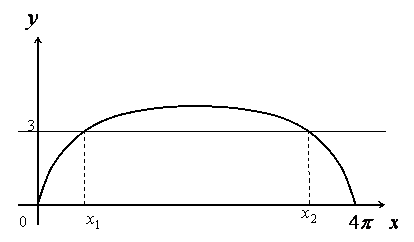
Это уравнения циклоиды (см. рис). Найдём её пересечения с прямой 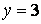 . Решая уравнение
. Решая уравнение 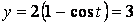 получим
получим 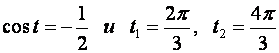 .
.
Искомая площадь фигуры равна
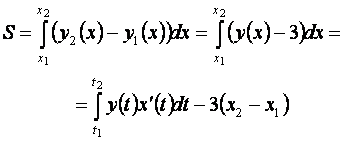
Подставим значения
 .
.
Площадь фигуры запишется
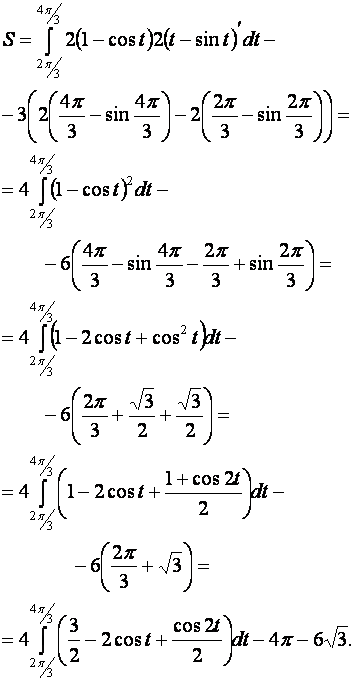
Вычислим определённый интеграл, используя формулу Ньютона-Лейбница. Тогда для площади фигуры получим:
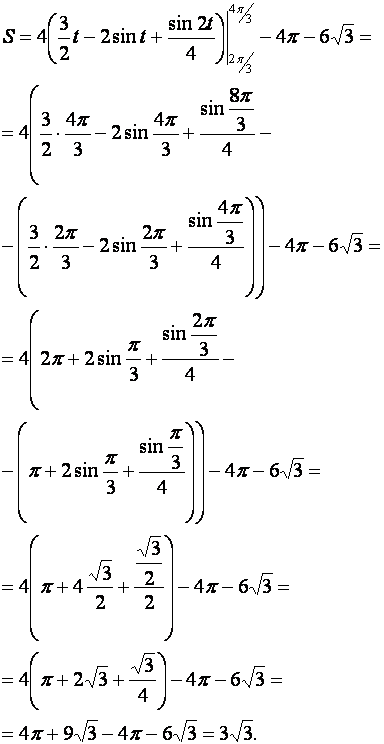
Ответ: 