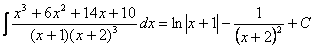Задача 6. Найти неопределённые интегралы.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

Решение

---

        6.4. Найти неопределённый интеграл    .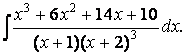

Решение.

        Разложим подынтегральную дробь на сумму простейших дробей:

        Приравниваем коэффициенты при одинаковых степенях в числителе:

        Решаем полученную систему

        Отсюда

        Таким образом, 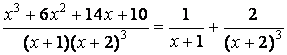  и   неопределённый интеграл запишется

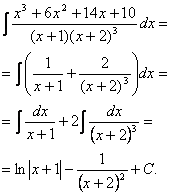
        Сделаем проверку, продифференцировав полученный неопределённый интеграл:

        Следовательно, неопределённый интеграл найден верно.

        Ответ:  

---