
Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
10.31. Привести квадратичную форму к каноническому виду методом Лагранжа.
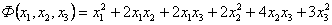
Решение.
Перепишем квадратичную форму в виде
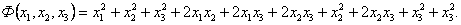
Заметим, что
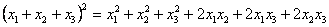
и
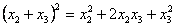 .
.Отсюда следует, что квадратичная форма запишется в виде
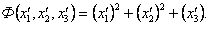
Переход к базису, в котором квадратичная форма имеет
канонический вид, осуществляется преобразованием 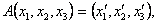 где
где
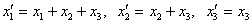 .
.Привести квадратичную форму к каноническому виду
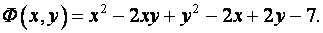
Решение.
Приведём квадратичную форму к каноническому виду по методу Лагранжа.
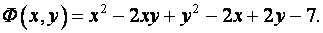
Три первых члена квадратичной формы представляют собой квадрат разности. Действительно,
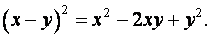
Тогда квадратичная форма запишется в виде:
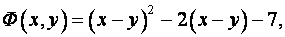
или в виде
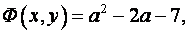
здесь a = x - y. Но (a-1)2 = a2 - 2a + 1. Следовательно,
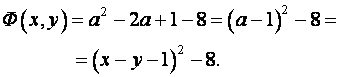
Итак, каноническая форма записи квадратичной формы
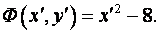
Здесь 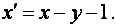 .
.