Задача 11. Привести квадратичную форму к каноническому виду ортогональным преобразованием.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
11.14. Привести квадратичную форму к каноническому виду ортогональным преобразованием.
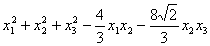.Решение.
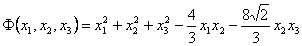. Найдём собственные числа и собственные векторы квадратичной формы.
Матрица квадратичной формы имеет вид
Составим характеристическое уравнение матрицы квадратичной формы
Подставляя в характеристическое уравнение матрицу квадратичной формы и единичную матрицу, получим характеристическое уравнение в следующем виде
Раскроем определитель, тогда характеристическое уравнение запишется в виде
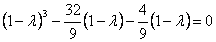
Приведём подобные слагаемые и вынесем общий множитель за скобки. Характеристическое уравнение матрицы квадратичной формы запишется
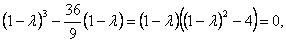
или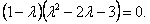 
Из полученного выражения находим корни характеристического уравнения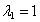 
или
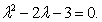
Дискриминант квадратного уравнения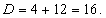 
Соответствующие корни
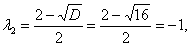
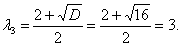
Таким образом, мы нашли корни характеристического уравнения матрицы заданной квадратичной формы. Эти корни являются собственными значениями квадратичной формы: ,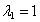 
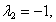
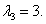
Канонический вид квадратичной формы
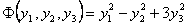
Найдём собственные векторы квадратичной формы. Для собственного вектора, соответствующего собственному значению 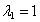, получим систему уравнений
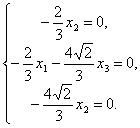
Из этой системы находим
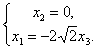
Собственный вектор
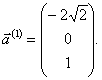
Для собственного вектора, соответствующего собственному значению 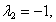, получим систему уравнений
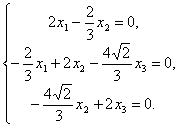
Из этой системы находим
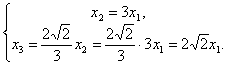
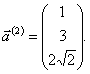
Для собственного вектора, соответствующего собственному значению 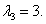, получим систему уравнений
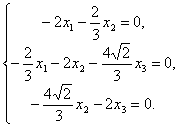
Из этой системы находим
Собственный вектор
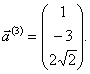
Найдём длины собственных векторов.
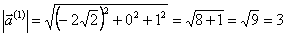
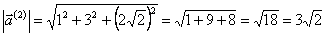
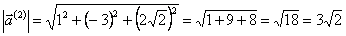
Нормируем собственные векторы, то есть найдём единичные векторы, соответствующие собственным векторам.
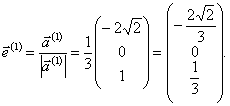
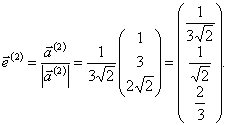
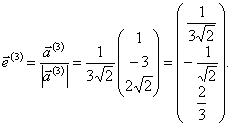
Запишем искомое ортогональное преобразование, приводящее квадратичную форму к каноническому виду.
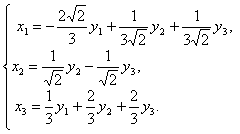
Ответ: Канонический вид квадратичной формы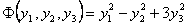
Ортогональное преобразование, приводящее квадратичную форму к каноническому виду