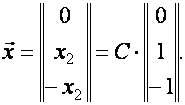Задача 9. Найти собственные значения и собственные векторы матрицы.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
9.31. Найти собственные значения и собственные векторы матрицы
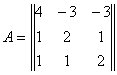
Решение.
Для того, чтобы найти собственные значения матрицы, их ещё называют собственные числа, cоставим характеристическое уравнение
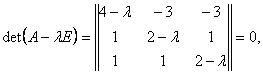
или
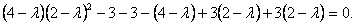 .
.Раскроем скобки и приведём подобные слагаемые. Собственные значения удовлетворяют уравнению
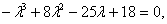
или
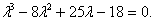 .
.Отсюда для собственных значений матрицы получаем уравнение
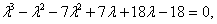
или уравнение
 .
.Вынесем общий множитель за скобки. Видим, что собственные значения довлетворяют уравнению
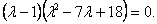
Произведение равно нулю, когда один из сомножителей равен нулю. Получаем совокупность уравнений
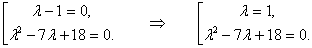
Второе уравнение анной совокупности — квадратное уравнение с отрицательным дискриминантом, 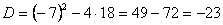 . Следовательно, оно не имеет действительных корней. Поэтому характеристическое уравнение имеет только один действительный корень
. Следовательно, оно не имеет действительных корней. Поэтому характеристическое уравнение имеет только один действительный корень 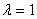 , а матрица только одно собственное значение
, а матрица только одно собственное значение 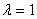 .
.
Найдём собственный вектор матрицы, принадлежащий этому собственному значению, решая уравнение
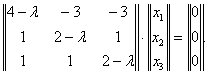
Расписывая по компонентам и подставляя 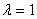 , получим систему из трёх уравнений с тремя неизвестными:
, получим систему из трёх уравнений с тремя неизвестными:
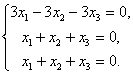
Второе и третье уравнения одинаковые. Поэтому систему можно переписать в виде:
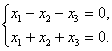
Сложим оба уранения, а затем из второго вычтем первое. Получим
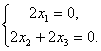
Отсюда
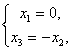
и мы имеем собственный вектор
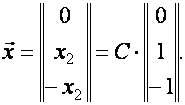
Ответ: Собственное значение 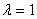 и собственный вектор матрицы
и собственный вектор матрицы