Задача 12. Найти модуль циркуляции векторного поля a вдоль контура Г.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        12.14. Найти модуль циркуляции векторного поля 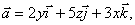вдоль контура Г

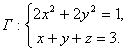
Решение.

        Согласно формуле Стокса циркуляция векторного поля определяется через ротор векторного поля:   . Здесь 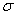— участок поверхности, ограниченный контуром 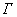, 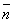— единичный вектор нормали к данной поверхности.
        Найдём ротор векторного поля

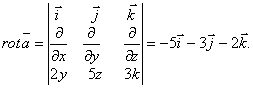
        С учётом этого циркуляция векторного поля запишется

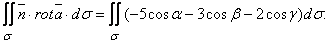
        Здесь 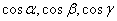    — направляющие косинусы нормали к поверхности или координаты единичного вектора нормали.
        Из общего уравнения плоскости запишем координаты нормального вектора 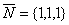    и найдём длину нормального вектора  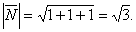 Тогда направляющие косинусы

.

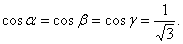          Элемент поверхности 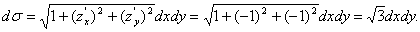Проекцией поверхности 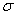на плоскость 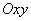является круг .
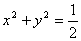        Этот круг имеет центр в начале координат и радиус 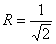.   Площадь данного круга

.

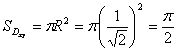        Перейдём от поверхностного интеграла к двойному. Циркуляция векторного поля

.

        Тогда модуль циркуляции векторного поля .
        Ответ: Модуль циркуляции векторного поля равен .