Задача 7. Найти поток векторного поля a через замкнутую поверхность S (нормаль внешняя).

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

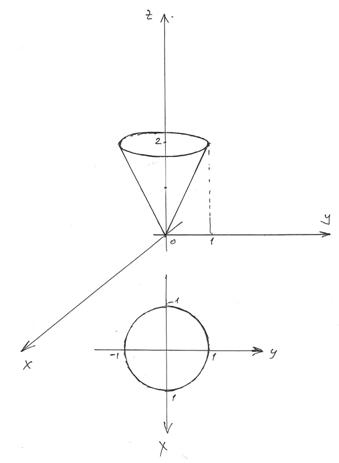
        7.14. Найти поток векторного поля a через замкнутую поверхность S (нормаль внешняя). $$ \vec a=(3x-2z)\vec i +(z-2y) \vec j +(1+2z) \vec k, \; S: z^2=4(x^2+y^2), z=2. $$

Решение.

        Поверхность \( S\) ограничивает конус, у которого радиус равен \(R=1\) и высота \(H=2\). Чтобы определить поток векторного поля через замкнутую поверхность, воспользуемся формулой Гаусса-Остроградского:$$ П=\iint_S (\vec a, \vec n)dS=\iiint_V div \vec a dxdydz. $$         Здесь $$ div \vec a = \frac{\partial a_x}{\partial x}+\frac{\partial a_y}{\partial y}+\frac{\partial a_z}{\partial z}=\frac{\partial (3x-2z)}{\partial x}+\frac{\partial (z-2y)}{\partial y}+\frac{\partial (1+2z)}{\partial z}=6-2+2=3 $$ — дивергенция векторного поля
        Поток векторного поля: $$ П=\iiint_V 3 dxdydz =3\iiint_V dxdydz. $$         Здесь \( V=\frac13 \pi R^2 H \) — объём конуса. Тогда поток векторного поля запишется: $$ П=3\cdot \frac{2\pi}3 =2\pi. $$         Ответ: Поток векторного поля равен \(П=2\pi\).

---