Задача 8. Найти поток векторного поля a через замкнутую поверхность S (нормаль внешняя).

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        8.13. Найти поток векторного поля a через замкнутую поверхность S (нормаль внешняя).   $$ \vec a = 6x \vec i-2y \vec j - z\vec k, $$ $$ S: \left\{\begin{matrix}z=3-2(x^2+y^2),\\ z^2=x^2+y^2 (z>0). \\ \end{matrix} \right. $$

Решение.

        Дивергенция векторного поля $$ div \vec a = \frac{\partial a_x}{\partial x}+\frac{\partial a_y}{\partial y}+\frac{\partial a_z}{\partial z}=\frac{\partial (6x)}{\partial x}-\frac{\partial (2y)}{\partial y}-\frac{\partial z}{\partial z}=6-2-1=3. $$         Чтобы найти поток векторного поля \(\vec a \) через замкнутую поверхность \(S\) используется формула Гаусса-Остроградского или формула Остроградского_Гаусса:$$ П=\iint_S (\vec a, \vec n)dS=\iiint_V div \vec a dxdydz. $$         В нашем случае поток векторного поля запишется $$ П=\iiint_V 3 dxdydz =3\iiint_V dxdydz. $$

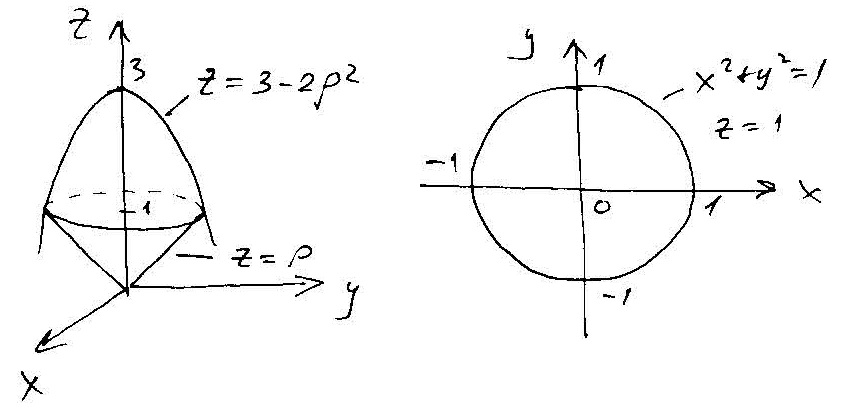
        Тело \(V\) ограничено двумя поверхностями. Сверху параболоидом вращения \(z=3-2(x^2+y^2)\), а снизу конусом \(z^2=x^2+y^2\). Найдём пересечение этих поверхностей, решая уравнение $$2z^2+z-3=0,$$ дискриминант которого равен \(D=1-4\cdot 2\cdot (-3)=25.\) Учитывая условие \(z>0\) получаем \(z=1\).

        Перейдём к цилиндрическим координатам по формулам: $$ x= \rho \cos \theta, \; y=\rho \sin \theta, \; z=z.$$         В цилиндрических координатах: уравнение конуса \( z=\rho \), уравнение параболоида вращения \( z=3-2\rho^2 \) и область интегрирования запишется в виде системы неравенств $$ V: \left\{\begin{matrix} 0 \le \theta \le 2\pi, \\ 0 \le \rho \le 1, \\ \rho \le z \le 3-2\rho^2. \\ \end{matrix} \right. $$         Тогда искомый поток векторного поля запишется $$ П=3 \int_0^{2 \pi} d\theta \int_0^1 \rho d\rho \int_{\rho}^{3-2\rho^2} dz =3\cdot 2 \pi \int_0^1 \rho (3-2\rho^2-\rho) d\rho = $$ $$ =6 \pi \int_0^1 (3\rho-2\rho^3-\rho^2) d\rho = 6 \pi \left. \left( {{3 \rho ^2 }\over 2}-{{2 \rho^4}\over 4} -{{\rho^3} \over 3} \right)\right|_0^1 = $$ $$ = 6 \pi \left( {3 \over 2}-{2 \over 4} -{1 \over 3} \right) = 6 \pi \cdot {2 \over 3}=4\pi .$$         Ответ: Поток векторного поля равен \(П=4\pi\).