

Задачи по физике
|
|
Уравнение прямой на плоскости
Каноническое уравнение прямой
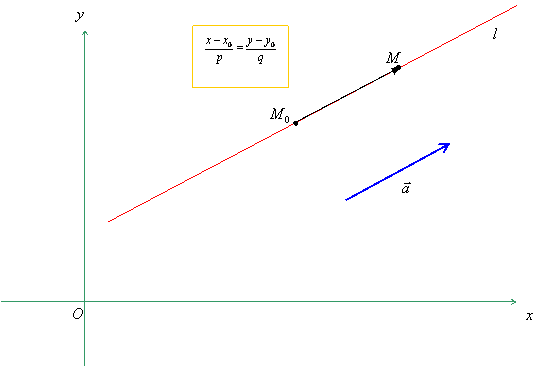
Пусть прямая l параллельна вектору a ={p,q} и проходит через точку M0(x0, y0) , тогда уравнение этой прямой может быть записано в виде
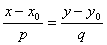 (1) (1)
Уравнение (1) называется каноническое уравнение прямой, а вектор a ={p, q} — направляющим вектором прямой l .
Легко убедится, что это действительно так. Рассмотрим произвольную точку прямой M(x, y) . Тогда вектор 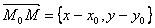 лежит на прямой l . Но прямая l параллельна вектору a ={p,q} . Следовательно, векторы лежит на прямой l . Но прямая l параллельна вектору a ={p,q} . Следовательно, векторы 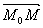 и a ={p,q} параллельны одной прямой, то есть они коллинеарные. Но тогда и a ={p,q} параллельны одной прямой, то есть они коллинеарные. Но тогда 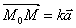 , или x − x0 = kp, y − y0 = kq. А отсюда следует, что , или x − x0 = kp, y − y0 = kq. А отсюда следует, что
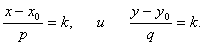
Приравнивая два последних равенства, получим уравнение (1).
Уравнение прямой, проходящей через две точки
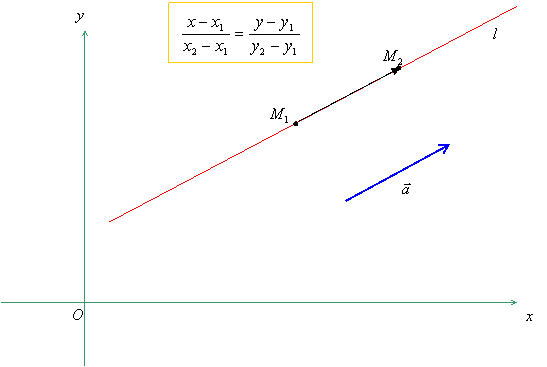
Если прямая l проходит через две точки M1(x1, y1) и M2(x2, y2), то её уравнение может быть записано в виде
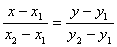 (2) (2)
В этом легко убедиться, если заметить, что вектор 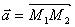 лежит на данной прямой, а, следовательно, коллинеарен ей. То есть вектор лежит на данной прямой, а, следовательно, коллинеарен ей. То есть вектор 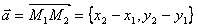 является направляющим вектором прямой l . Кроме того, прямая l проходит через точку M1(x1, y1) . Применяя к этой прямой уравнение (1) и учитывая, что p = x2 − x1 , q = y2 − y1, получим уравнение (2). является направляющим вектором прямой l . Кроме того, прямая l проходит через точку M1(x1, y1) . Применяя к этой прямой уравнение (1) и учитывая, что p = x2 − x1 , q = y2 − y1, получим уравнение (2).
Параметрические уравнения прямой
Так как в уравнении (1) обе дроби равны, то они равны одному и тому же числу . Поэтому уравнение (1) можно переписать в виде
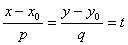
Отсюда получим систему
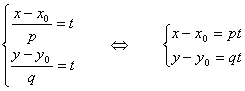
Отсюда получаем параметрические уравнения прямой.
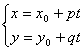 (3) (3)
Здесь, как и в (1), a ={p,q} — направляющий вектор, а M0(x0, y0) — произвольная точка, через которую проходит прямая.
Уравнение прямой, проходящей через точку M0(x0, y0) и перпендикулярной вектору N ={A, B} .
A·(x − x0) + B·( y − y0) = 0 (4)
Убедимся, что так и есть. Рассмотрим произвольную точку прямой M(x, y) . Тогда вектор 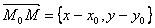 лежит на прямой l. Следовательно, вектор лежит на прямой l. Следовательно, вектор 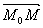 перпендикулярен вектору N ={A, B}. Но если векторы перпендикулярны, то их скалярное произведение равно нулю, то есть перпендикулярен вектору N ={A, B}. Но если векторы перпендикулярны, то их скалярное произведение равно нулю, то есть 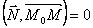 .
Раскрывая скалярное произведение, как сумму произведений соответствующих координат, получим выражение (4). .
Раскрывая скалярное произведение, как сумму произведений соответствующих координат, получим выражение (4).
Вектор N ={A, B} называется нормальный вектор прямой.
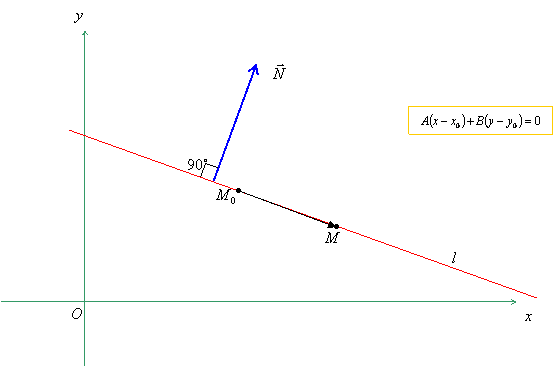
Общее уравнение прямой
Общее уравнение прямой это уравнение прямой вида
A·x + B· y + C = 0 (5)
Общее уравнение прямой легко получить из уравнения (4), если раскрыть скобки и привести подобные слагаемые.
Нормальное уравнение прямой
Нормальное уравнение прямой это уравнение прямой вида
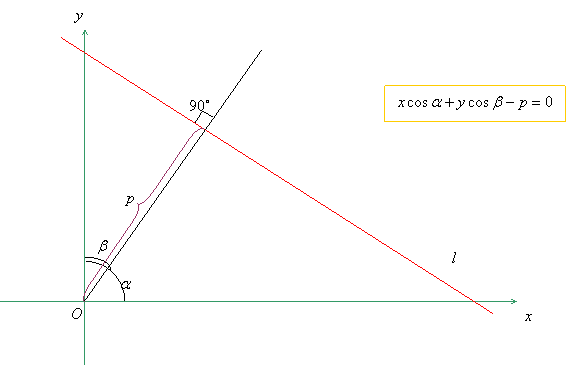
x·cosα + y· cosβ − p = 0. (6)
Здесь p — длина перпендикуляра, опущенного из начала координат на данную прямую – расстояние от начала координат до прямой. α, β — углы, образованные перпендикуляром с осями координат.
Нормальное уравнение прямой можно получить из общего уравнения прямой. Для этого, общее уравнение (5) необходимо умножить на нормирующий множитель
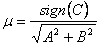 Здесь sign(C) = ± 1 — знак C. Принимаем sign(C) = 1, если C > 0 . Если C < 0 , то sign(C) = −1 . Величины A, B, C это коэффициенты общего уравнения (5). Здесь sign(C) = ± 1 — знак C. Принимаем sign(C) = 1, если C > 0 . Если C < 0 , то sign(C) = −1 . Величины A, B, C это коэффициенты общего уравнения (5).
Уравнение прямой в отрезках
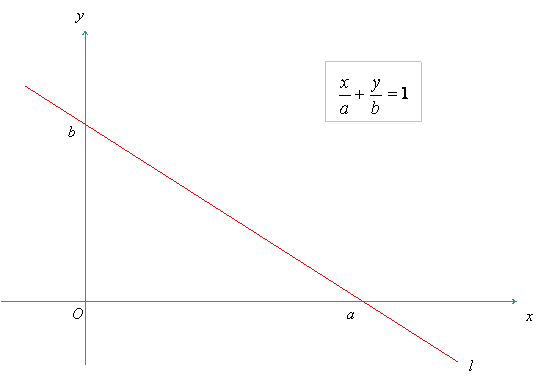
Если прямая отсекает на осях координат x, y отрезки a и b соответственно, то её уравнение может быть записано в виде
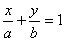 (7) (7)
Это уравнение получается из общего уравнения, если в общем уравнении (5) перенести C вправо, а затем поделить обе части уравнения на − C. При этом 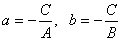 . .
Неполные уравнения прямой
Если прямая проходит через начало координат, то C = 0 и общее уравнение прямой имеет вид
A·x + B· y = 0.
Если прямая параллельна оси Ox , то A = 0 и её общее уравнение прямой имеет вид
B·y + C = 0, или y = y0.
Если прямая параллельна оси Oy, то B = 0, то и её общее уравнение прямой имеет вид
A·x + C = 0, или x = x0.
Уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом называется уравнение вида
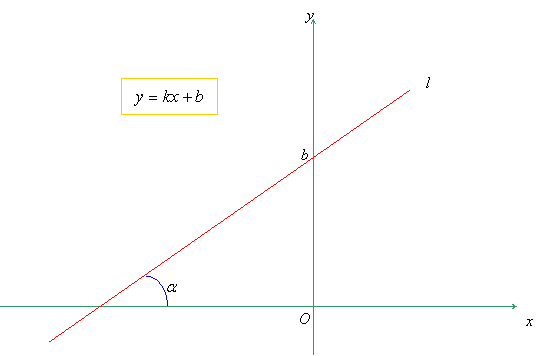
y = k·x + b. (8)
Здесь k = tgα, а α — угол, образованный прямой с положительным направлением оси абсцисс Ox . Величина b равна координате пересечения прямой с осью ординат Oy.
Это уравнение легко получается из любого уравнения. Для этого необходимо из взятого уравнения выразить y через x .
|
|
|



