Математические методы в экономике

        Решаем задачи из раздела математические методы в экономике. Быстро, качественно и недорого. Решение, по Вашему желанию, оформляется в Word. Гарантия качества и правильности.
Задачи присылайте по электронной почте:

      E-MAIL:          

      Ниже приведён пример решения задачи из раздела математические методы в экономике.

        Задача 1. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея $6 и $10 с вероятностями 1/3 и 2/3 и лотерея $3 и $9 с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?

Решение

        Полезность фон Неймана–Моргенштерна для двух благ можно представить в виде:

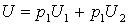   , где        .

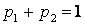В первой игровой ситуации:

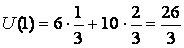
во второй игровой ситуации

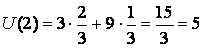
        Функционал риска, как известно, является линейным относительно суммы риска:

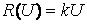
причем 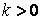        , поэтому для объективного риска выполняться соотношение  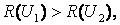   ибо

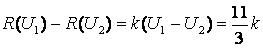
в данном случае. Однако обе лотереи для индивида эквивалентны, из чего следует, что для получения дополнительной пользы в виде дополнительной прибыли он склонен к необоснованному риску. Сумма его необоснованного риска в данном случае

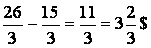
Поскольку указанная сумма больше минимального из значений лотерейных выигрышей (3 $ во второй лотерее), то индивид, безусловно, имеет существенную склонность к риску.

      Задача 1 из раздела математические методы в экономике полностью решена.


      Задача 2. Предпочтения судовладельца описываются функцией полезности типа Неймана—Моргенштерна с элементарной функцией полезности от богатства х вида u(х), причем u имеет положительную убывающую производную. Он владеет богатством $250 000 и может потерять в случае аварии судна $50 000. Вероятность аварии равна 0,03 и известно, что он застраховался на сумму $100 000. Возможно ли, что цена страхования на $1 равна $0,03? Если нет, то больше или меньше, чем $0,02? Объясните.

Решение

        Пусть элементарная функция полезности судовладельца имеет вид u(W) = ln(W). Богатство его в обычном состоянии (без аварии, в тысячах долларов) составляет 250, а при аварии он несет ущерб в размере 50 тыс, так что в результате аварии богатство составит 200 тыс. Вероятность аварии равна 0,03. Судовладелец застраховал свое имущество, при этом если x — страховая сумма, а γ — цена страховки, то богатство без аварии и при аварии равно, соответственно, W₁=250-γx и W₂=200+(1-γ)x .
      Ожидаемая полезность в данной ситуации имеет вид

U(x)=0,03ln(200+(1-γ)x+0,97ln(250-γx) .

        При x=100 (данная страховая сумма), из соображений полезности (судовладелец решил-таки страховаться) имеем:

U(100)=0,03ln(300-100γ)+0,97ln(250-100γ) > U(0) = 0,03ln200+0,97ln250.             (*)

        Поскольку функция полезности имеет положительную убывающую производную, то она является вогнутой функцией, а поэтому из последнего неравенства вытекает, что при возрастании γ разность между частями неравенства (*) убывает.
      Подставим в (*) γ=0,03 ; получим:

        Поскольку последнее неравенство истинно, то вполне возможно, что цена страхования на $1 равна $0,03 (и даже чуточку выше!).

      Задача 2 из раздела математические методы в экономике полностью решена.


      Задача 3. Найти объем продукции, выпущенной предприятием за год (258 рабочих дней), если ежедневная производительность этого предприятия задана функцией

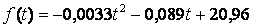
где 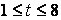        — время в часах.

Решение

        Искомый годовой объем продукции

       Задача 3 решена полностью.



     Ещё образцы решения задач по математическим методам в экономике

      Как видим математические методы нужны не только при решениии задачи по физике, но и при решении экономических задач.


      Образцы решения задач по математическим методам в экономике

      Математика для студентов заочной формы обучения.

      Решение задач по физике на заказ

      МАТЕМАТИКА

      Линейное программирование

      Математические методы в экономике