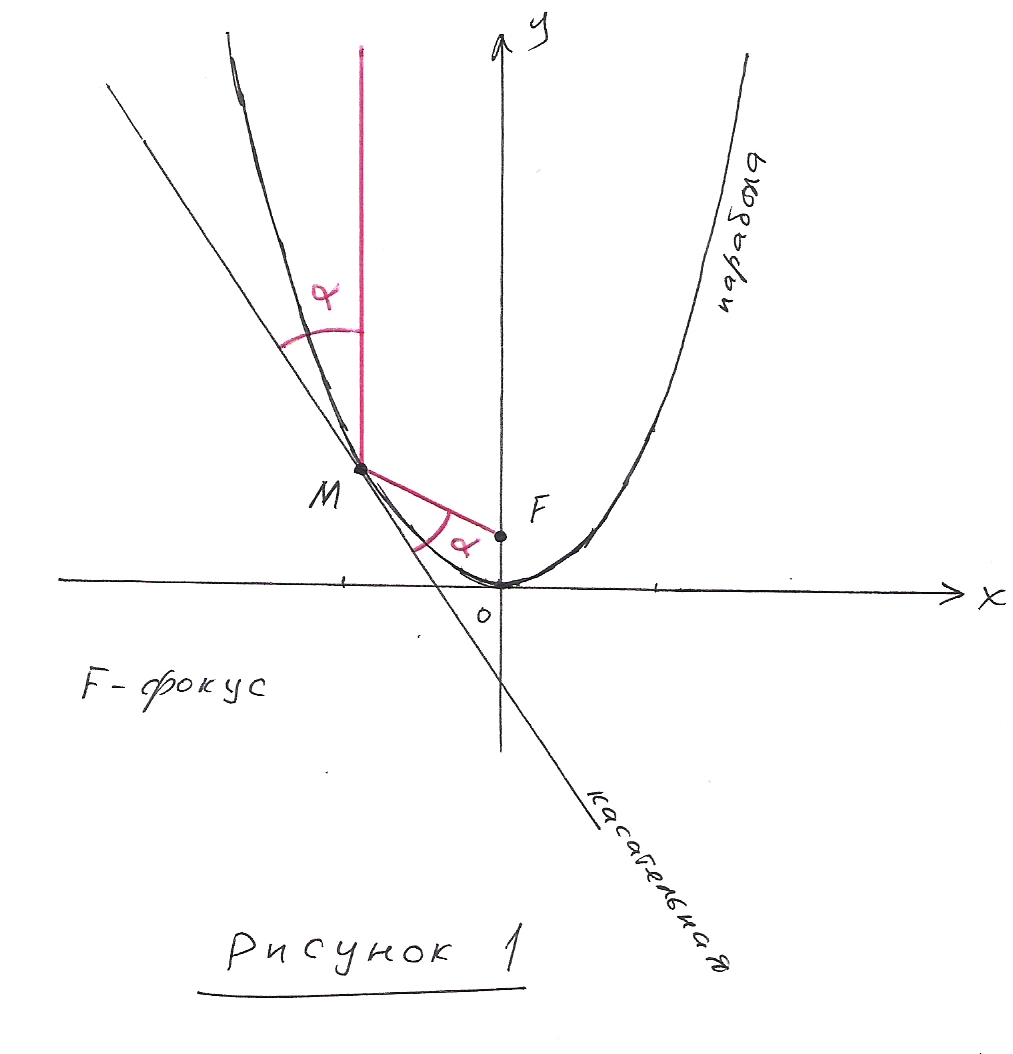
Рассмотрим параболу y = x 2, точку F( 0; 1/4 ) и горизонтальную прямую L, имеющую уравнение y = - 1/4. Смотри рисунок 1. Возьмём произвольную точку M(x;y), лежащую на параболе. Так как точка M лежит на параболе, то её координаты удовлетворяют уравнению параболы. То есть y = x 2. Поэтому координаты точки M( x; y 2).
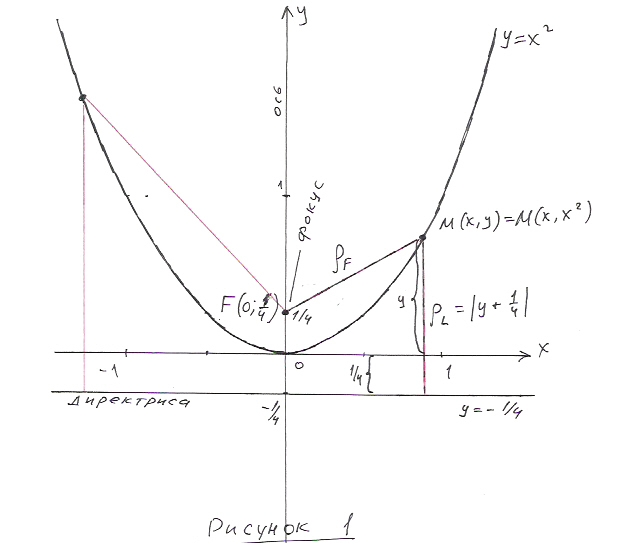
Найдём расстояние от точки M до точки F.
Теперь найдём расстояние от точки M до прямой L. Как видно из рисунка это расстояние равно сумме ординаты точки M и 1/4. То есть, расстояние до прямой равно
ρL = y + 1/4 = x 2 + 1/4 .
Таким образом, найденные расстояния равны. То есть, для любой точки параболы ρM = ρL .
Это фундаментальное геометрическое свойство любой параболы.
То есть, для любой параболы существует такая точка, называемая фокусом, и такая прямая, называемая директрисой, что расстояние от произвольной точки параболы до фокуса и до директрисы одинаковы.
Например, для параболы x = – y2 фокусом является точка F(-1/4; 0 ) , а директрисой прямая x = 1/4. Смотри рисунок 2.
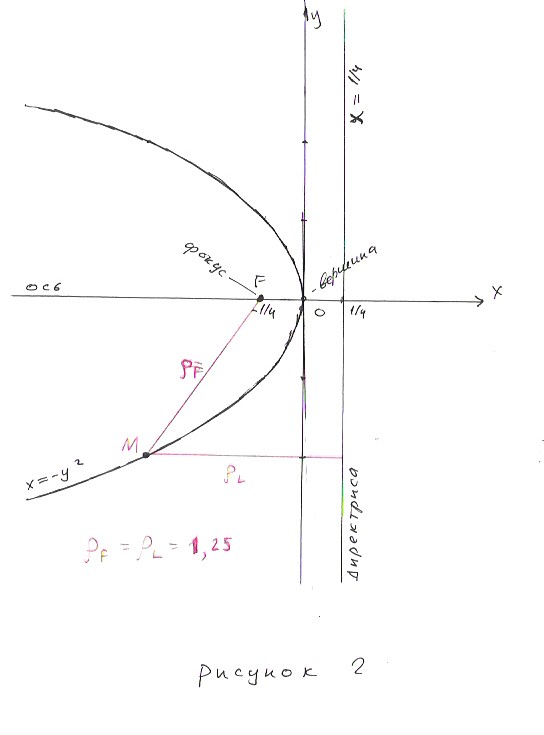
Ось параболы это её ось симметрии. Фокус находится на оси параболы, а директриса перпендикулярна оси. Фокус находится внутри параболы, а директриса вне её.
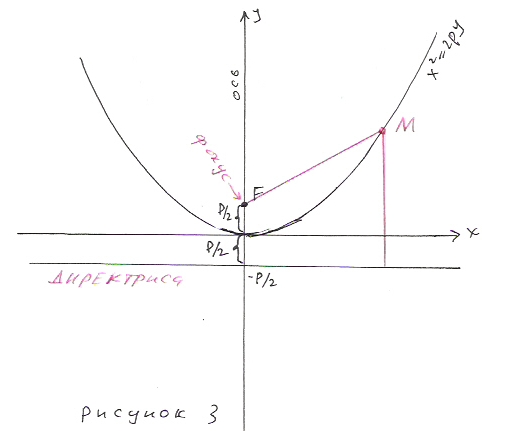
Если парабола имеет уравнение
x2 = 2py (1)
или
y2 = 2px (2)
то число p называется параметром параболы.
Уравнения (1) и (2) называются каноническими уравнениями параболы.
Фокус и директриса удалены от вершины на одинаковое расстояние p/2. Смотри рисунки 3.
Найдём фокус и директрису для параболы y = ax2 + bx+c. Для этого приведем это уравнение к каноническому виду (1).
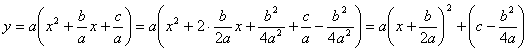
Отсюда находим координаты вершины A:
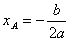и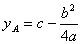 
С другой стороны, разделив на a, получим
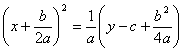
или
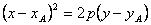
Здесь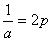 
. Из этого условия найдём параметр параболы 
.
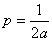Ось параболы — вертикальная прямая, проходящая через вершину A.
Фокус лежит на оси на расстоянии p/2 от вершины. Следовательно, координаты фокуса
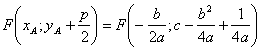
То есть, фокус параболы имеет координаты
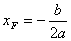
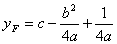
Теперь, напишем уравнение директрисы. Так как ось вертикальна, то директриса горизонтальна. Её уравнение
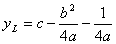
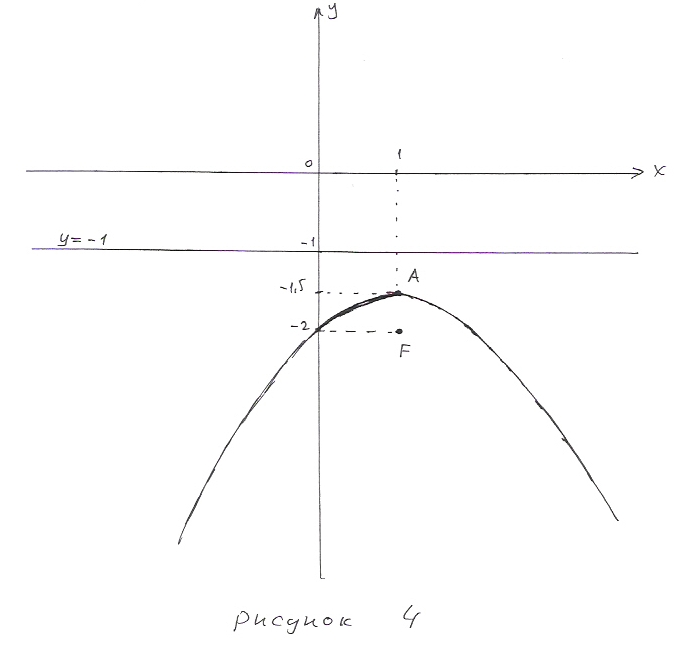
Пример: Построить параболу y = - 0,5x2 + x – 2. Найти её фокус и директрису.
Решение. Имеем a = - 0,5; b = 1; c = -2.
Координаты вершины xA = 1, yA = - 2 + 0,5 = - 1,5.
Координаты фокуса xF = 1, yF = - 2 + 0,5 – 0,5 = - 2.
Ординаты точек директрисы yL = - 2 + 0,5 + 0,5 = - 1. Поэтому, уравнение директрисы y = - 1. Построение на рисунке 4.
Оптическое свойство параболы. Параболоид инженера Гарина
Сначала сформулируем одно геометрическое свойство параболы. Смотри рисунок 1.
Касательная к параболе в некоторой точке M составляет равные углы с фокальным радиусом FM и с лучом, исходящим из точки M и параллельным оси параболы.
В оптике (науке о свете) есть закон отражения. Смотри рисунок 2.
Падающий и отражённый лучи образуют равные углы с отражающей поверхностью.
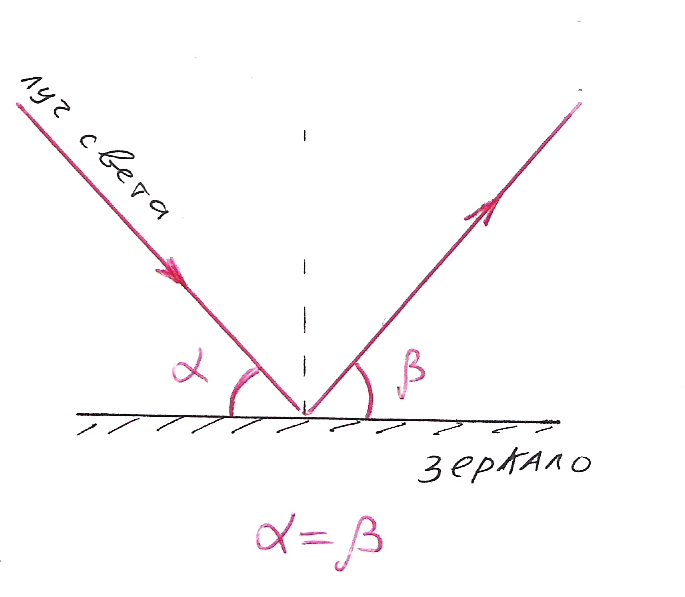
Теперь представим, что луч света находится в той же плоскости, что и парабола. Представим, что парабола изнутри зеркальная и поразмышляем.
Если луч света выходит из фокуса, то, отразившись от параболы, он пойдёт параллельно оси. Это следует из закона отражения и свойства параболы.
Смотри рисунок 3.
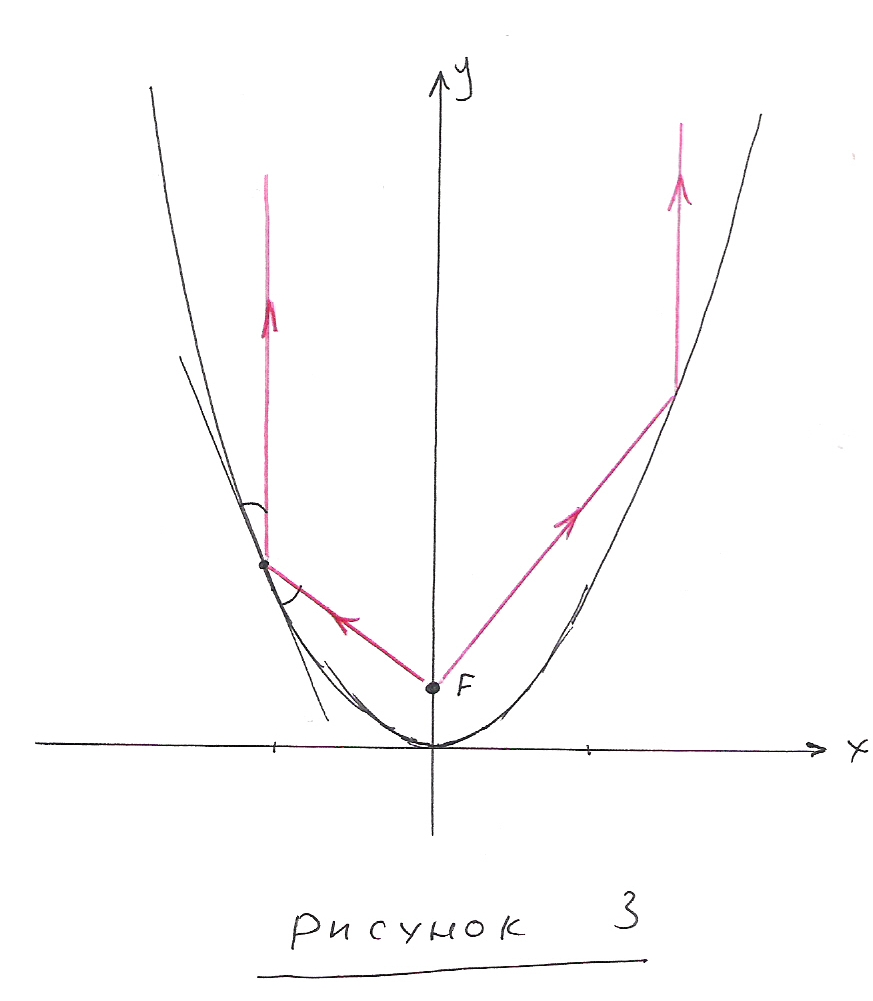
Если луч, идущий параллельно оси параболы падает на её зеркальную внутреннюю сторону, то, отразившись далее, он пройдёт через фокус. В итоге, если плоский пучок света, параллельный её оси, падает на параболу изнутри, то все лучи, отразившись от неё, изменят направление на фокальное. То есть, соберутся в фокусе.
Смотри рисунок 4.
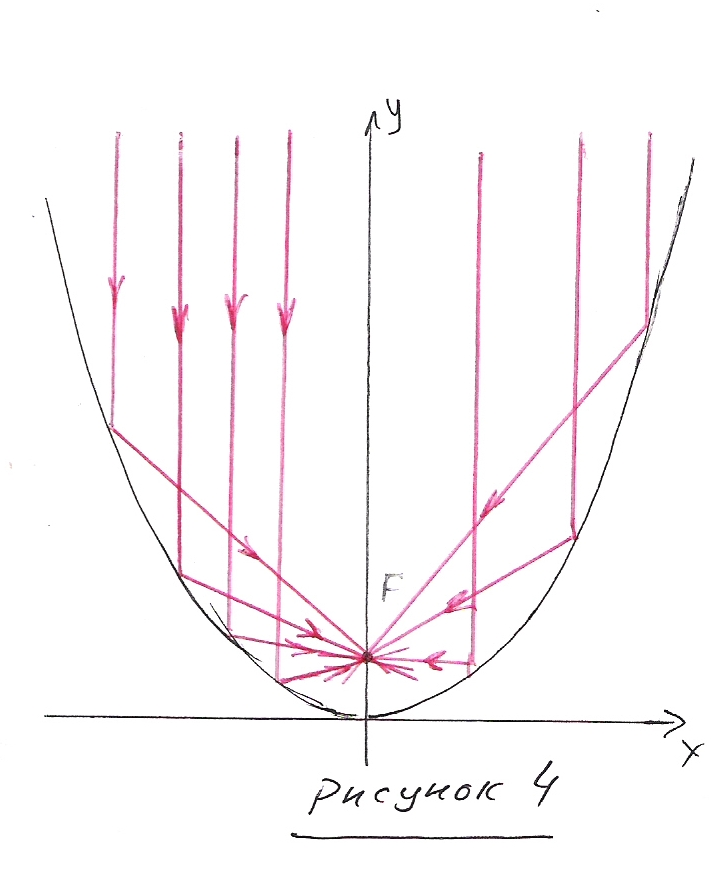
Поверхность, получающаяся при вращении параболы вокруг своей оси, называется параболоидом вращения. Смотри рисунок 5. Так как парабола одна, просто она поворачивается вокруг своей оси, то фокус будет один. Фокус параболоида вращения совпадает с фокусом самой вращающейся параболы.
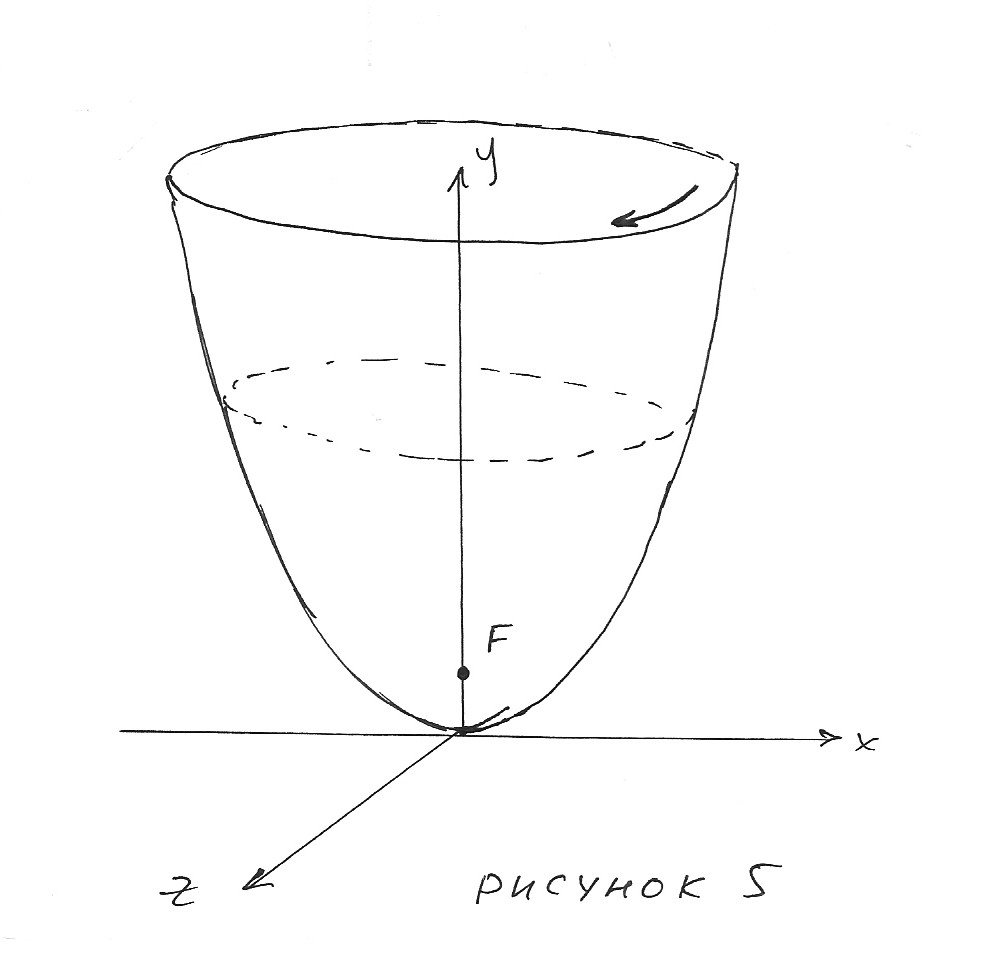
Поскольку параболоид вращения образован параболами, то он обладает тем же оптическим свойством. На этом свойстве параболы и параболоида вращения основано устройство прожекторов.
В фокусе зеркала, изготовленного в виде параболоида вращения, помещается источник света (нить накаливания). Лучи света от этого источника отражаются от зеркальной поверхности параболоида и направляются параллельно оси параболоида. В результате получается параллельный пучок света.
Лампочка светит во всех направлениях. Это удобно для освещения помещения. Но иногда требуется направленный пучок света. Например, для фар автомобиля, или для маяка, или для прожектора на границе. Прожектор может освещать очень отдалённые объекты, поскольку световая энергия не рассеивается во всех направлениях, а сосредоточена в узком пучке.
Иногда необходимо, наоборот, собрать параллельный пучок света в одной точке – фокусе. Например, параболические зеркала используют в телескопах. Такие телескопы называются рефлекторы.
У Алексея Толстого есть роман “Гиперболоид инженера Гарина”. Главный герой инженер Гарин изобретает оружие, с помощью которого собирается захватить весь Мир. А. Толстой неправильно называет его “гиперболоидом”. Правильно было бы назвать “Параболоид инженера Гарина”.
