
Здесь рассмотрено несколько интересных задач по физике преимущественно из разделов механики и термодинамики.
С какой силой атмосфера давит на человека?
Площадь поверхности человека \(S=1,7\,м^2.\) Атомсферное давление равно \(p=10^5\, Па.\) Сила давления$$F=pS=1,7\,м^2\cdot10^5\,Па=1,7\cdot10^5Н.$$ Много это или мало? С такой силой давит груз массой$$m=\frac Fg=\frac{1,7\cdot10^5Н}{9,8\,м/с^2}=17346\,кг.$$ То есть на взрослого человека давит семнадцать с лишним тонн — это примерно пять слонов или грузовой автомобиль.
Какая плотность воздуха при нормальных условия?
Из уравнения Менделеева-Клапейрона$$pV=\frac m\mu RT$$найдём плотность$$\rho=\frac mV=\frac{p\mu}{RT}.$$Здесь: \(\mu=0,029\,кг/моль\) — молярная масса воздуха; \(R=8,31\,Дж/К\cdot моль\) — универсальная газовая постоянная;
\(T=0^oC=273\,К\) — температура при нормальных условиях; \(p=10^5\,Па\) — нормальное атмосферное давление. Подставляя эти значения в формул для плотности воздуха, получим$$\rho=\frac{10^5\,Па\cdot0,029\,кг/моль}{8,31\,Дж/К моль\cdot273\,К}=1,28\frac{кг}{м^3}.$$ Таким образом в комнате с объёмом 50 кубометров (площадью 20 кв.м и высотой потолков 2,5 м) находится примерно 60 кг воздуха.
Задача о минимальной массе воздушного шара.
Воздушный шар наполяется гелием при при нормальных условиях. Один квадратный метр материала оболочки шара имеет массу 3кг. Каким должна быть минимальная масса шара, чтобы он смог подняться в воздух?
Дано: \(\sigma=3\,кг/м^2\); \(T=0^oC=273\,К\); \(p=1\,атм=10^5\,Па\). Найти: \(m_{min}=?\)
Решение.
На шар действует сила тяжести \(mg\), направленная вертикально вниз, и выталкивающая сила Архимеда \(F_A=\rho_0gV\), направленная вертикально вверх. Здесь \(V\) — объём шара, а \(\rho_0\) плотность окружающего его воздуха. Масса шара состоит из массы оболочки, которая равна \(\sigma S\), и массы наполняющего её гелия, которая равна \(\rho V\). Таким образом$$\qquad\qquad\qquad\qquad\qquad\qquad m=\sigma S+\rho V, \qquad\qquad\qquad\qquad\qquad\qquad(1)$$где \(\rho\) — плотность гелия, а \(S\) — площадь оболочки шара.
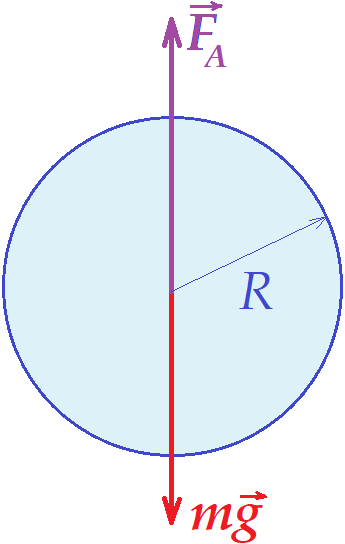
Шар начнёт подниматься, когда сила Архимеда превзойдёт силу тяжести, то есть при условии \(F_A\gt mg\) или$$\rho_0gV\gt(\sigma S+\rho V)g.$$Отсюда после сокращения на ускорение свободного падения \(g\) и последующего преобразования получим$$(\rho_0-\rho)V\gt\sigma S.$$ Из курса геометрии шаров и сфер нам стало известно, что объём и площадь поверхности шара определяются формулами$$V=\frac43\pi r^3, \qquad \qquad S=4\pi r^2.$$ Подставим \(V\) и \(S\) в последнее неравенство и сократим его на \(4\pi r^2\). В результат этих действий получим$$(\rho_0-\rho)\frac r3\gt\sigma.$$Отсюда$$r\gt\frac{3\sigma}{\rho_0-\rho}.$$ Таким образом, минимальный радиус шара, при котором он сможет подниматься, равен$$r_{min}=\frac{3\sigma}{\rho_0-\rho}.$$ Подставим в формулу (1) выражение для объёма \(V\) и площади поверхности \(S\) найдём минимальную массу.$$m_{min}=4\pi r_{min}^2\left(\sigma +\frac{\rho r_{min}}3\right).$$ Подставим найденное значение минимального радиуса. После преобразования получим$$m_{min}=\frac{36\pi\rho\sigma^3}{(\rho_0-\rho)^3}.$$
Из этой формулы мы видим, для того чтобы подняться шар должен быть достаточно тяжёлым \((m\gt m_{min}).\) Лёгкий шар, масса которого меньше минимальной, не сможет подняться. Что в целом противоречит не только расхожему мнению, но и мнению Аристотеля, считавшего, что тяжёлые тела должны падать вниз, а лёгкие подниматься вверх. На данном примере мы видим, что всё происходит с точностью до наоборот.
Однако вернёмся к вычислению массы. Нам осталось посчитать плотность воздуха и гелия и подставить их в формулу массы. Из уравнения Клапейрно-Менделеева, плотность газа равна$$\rho=\frac mV=\frac{p\mu}{RT}.$$Тогда$$m_{min}=\frac{36\pi \mu R^2T^2\sigma^3}{p^2(\mu_0-\mu)^3}.$$Здесь: \(R=8,31\,Дж/К\cdot моль\) — универсальная газовая постоянная; \(\mu_0=0,029\,кг/моль\) — молярная масса воздуха; \(\mu=0,004\,кг/моль\) — молярная масса гелия.
Подставим значения в формулу минимальной массы и посчитаем её на калькуляторе.$$m_{min}=\frac{36\pi 0,004\,кг/моль \left(8,31\,Дж/Кмоль \right)^2(273\,К)^2\left(3\,кг/м^2 \right)^3}{\left(10^5\,Па\right)^2\left(0,029\,кг/моль-0,004\,кг/моль\right)^3}=402,33\,кг.$$ Ответ: \(m_{min}=402\,кг\).
Итак, минимальная масса воздушного шара равна почти полтонны!
ЗАДАЧА. Какая установится температура в каллориметре, если в него поместить лёд при \(0^oC\) и пар при \(100^oC\) одинаковой массы?
Дано: \(c=4200\,Дж/(кг\cdot K)\); \(\lambda=3,3\cdot10^5\,Дж/кг\); \(T_1=0^oC=273\,К\); \(r=2,3\cdot10^6\,Дж/кг\); \(T_2=100^oC=373\,К\).
Найти: \(T=?\)
Решение.
При конденсации пара выделяется тепло$$Q_п=mr=2,3\cdot10^6m.$$
При плавлении льда поглощается тепло$$Q_л=m\lambda=3,3\cdot10^5m.$$
Следовательно, энергии пара хватит чтобы полностью расплавить лёд. Найдём, сколько потребуется тепла для нагревания растаявшей воды до температуры пара.$$Q_в=mс(T_2-T_1)=m\cdot4200\cdot100=4,2\cdot10^5m.$$ Сравнивая найденные величины, находим, что
$$Q_л+Q_в=m\lambda+mс(T_2-T_1)=7,5\cdot10^5m\lt2,3\cdot10^6m=Q_п.$$ Таким образом, теплота, выделившаяся при конденсации всего пара значительно превосходит теплоту, необходимую для плавления всего льда и доведения растаявшей воды до температуры кипения. Из чего следует, что только часть теплоты всего пара понадобится для плавления льда и доведения воду до температуры \(100^oC,\) а значит какая-то часть пара останется. Но пар и вода могут находится в каллориметре только при \(100^oC.\)
Ответ: \(T=100^oC.\)
ЗАДАЧА. Найти массу пара, находящегося при температуре \(100^oC\), необходимую для того, чтобы полностью растопить лёд массой \(1 \,кг,\) находящийся при \(0^oC?\)
Дано: \(m=1кг\); \(T_1=0^oC\); \(\lambda=3,3\cdot10^5\,Дж/кг\); \(r=2,3\cdot10^6\,Дж/кг\); \(T_2=100^oC\).
Найти: \(m_п=?\)
Решение.
При конденсации пара выделяется тепло \(Q_п=m_пr.\) Кроме этого при остывании воды выделится ещё \(Q_в=m_пct=100m_пc.\) Совокупное тепло, полученное от пара равно: \(Q=Q_п+Q_в=m_п(r+100c).\) При плавлении льда поглощается тепло \(Q_л=m\lambda.\) Из уравнения теплового баланса получаем: \(Q=Q_л\) или \(m_п(r+100c)=m\lambda.\) Отсюда$$m_п=\frac{m\lambda}{r+100c}.$$ Подставим данные и посчитаем.$$m_п=\frac{1кг\cdot3,3\cdot10^5Дж/кг}{2,3\cdot10^6Дж/кг+100\cdot4200Дж/кг}=0,121\,кг=121\,гр.$$ Ответ: \(m_п=121\,гр.\)
ЗАДАЧА. Найти массу пара, находящегося при температуре \(100^oC\), необходимую для того, чтобы полностью растопить лёд массой \(1\, кг\), находящийся при температуре \(0^oC,\) и довести его до кипения?
Дано: \(m=1кг\); \(T_1=0^oC\); \(c=4200\,Дж/(кг\cdot K)\); \(\lambda=3,3\cdot10^5\,Дж/кг\); \(r=2,3\cdot10^6\,Дж/кг\); \(T=100^oC\).
Найти: \(m_п=?\)
Решение.
При конденсации пара выделяется тепло \(Q_п=m_пr.\) При плавлении льда и последующем нагревании растаявшей воды поглощается тепло $$Q=m\lambda+mc(T_2-T_1).$$ Из уравнения теплового баланса получаем: \(Q_п=Q\) или$$m_пr=m\lambda+mc(T_2-T_1).$$Отсюда$$m_п=\frac{m(\lambda+c(T_2-T_1)}r.$$ Подставим данные и посчитаем.$$m_п=\frac{1кг\cdot(3,3\cdot10^5Дж/кг+4200Дж/(кг\cdot К)\cdot 100^oC)}{2,3\cdot10^6Дж/кг}=0,326\,кг=326\,гр.$$ Ответ: \(m_п=326\,гр.\)
ЗАДАЧА. Найти радиус металлического шара, электрическая ёмкость которого равна \(1\,Ф.\)
Дано: \(C=1\,Ф.\) Найти: \(R=?\)
Решение.
Электрическая ёмкость сферического конденсатора определяется соотношением$$C=\frac q\varphi=4\pi\varepsilon_0 R.$$ Отсюда радиус металлического шара равен $$R=\frac C{4\pi\varepsilon_0}=\frac {1\,Ф}{4\pi8,85\cdot10^{-12}\,Ф/м}=9\cdot10^9\,м.$$ Ответ: \(R=9\cdot10^9\,м.\)
Это 9 миллионнов километров! Много это или мало судите сами? Например, это в 1411 раз больше радиуса Земли, и в 23,4 раза больше, чем расстояние от центра Земли до центра Луны! Земля в сравнении с этим шаром меньше микрофарады.
ЗАДАЧА. Найти длину стороны квадратных пластин, расположенных на расстоянии 1 метр друг от друга и составляющих плоский конденсатор, электическая ёмкость которого равна \(1\,Ф.\)
Дано: \(C=1\,Ф;\) \(d=1\,м.\) Найти: \(a=?\)
Решение.
Электрическая ёмкость плоского конденсатора равна$$C=\frac{\varepsilon_0S}d,$$где \(S=a^2\) — площадь каждой квадратной пластины.
Таким образом$$C=\frac{\varepsilon_0a^2}d.$$
Отсюда длина стороны пластины равна $$a=\sqrt{\frac{Cd}{\varepsilon_0}}=\sqrt{\frac{1Ф\cdot1м}{8,85\cdot10^{-12}\,Ф/м}}=336146\,м.$$ Ответ: \(R=336\,км.\)
Если электроёмкость конденсатора составляет 1 фараду, то его размеры огромны. Даже если мы уменьшим расстояние между платинами до 1 миллиметра, то его размеры будут составлять 10 километров 630 метров. А если пластины сблизить до толщины одного листа офисной бумаги, поместив между ними бумагу, чтобы металлические платины не касались друг друга, то размеры такого конденсатора будут равны 2 киллометра 226 метров. Вот что такое фарада, и вот почему конденсаторов с электрической ёмкостью в одну фараду не существует.
