
Рассмотрим несколько задач по физике и их решения. Предлагаемая, в качестве первой, задача по физике, вероятно, не покажется слишком сложной.
Задача
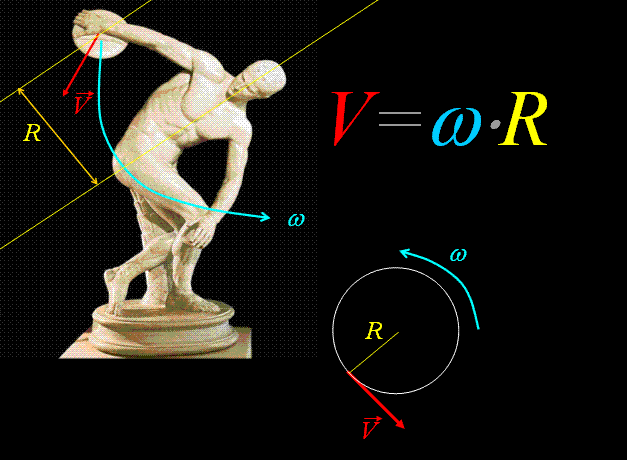
Найти линейную скорость диска, если его угловая скорость составляет 3 радиана в секунду. Считать, что диск движется по окружности радиуса 1 метр.
Решение
Линейная скорость \(v\) и угловая скорость \(\omega\) связаны соотношением$$v=\omega \cdot R.$$Здесь \(R=1 м\) — радиус окружности. Таким образом,$$v=3 рад/c \cdot 1 м=3 м/c.$$ Ответ: \(v=3 м/c.\)
Следующая задача по физике также является довольно простой.
Задача
С каким ускорением движется тело массой 2 килограмма, если к нему приложена сила 10 ньютонов. Просьба пренебречь силами сопротивления.
Решение
По второму закону Ньютона$$F=m\cdot a.$$ Отсюда для ускорения получим$$a=\frac Fm.$$ Подставим в полученное выражение данные. Тогда $$a=\frac{10Н}{2кг}=5\frac м{c^2}.$$ Ответ: \(a=5м/c^2.\)
В задачах по физике иногда требуется рисунок. Рассмотрим следующую задачу по физике.
Задача
Брусок движется по наклонной плоскости с углом наклона
Решение
На брусок действуют следующие силы: сила тяжести \(m\cdot \vec g\), направленная вниз; cила реакции опоры \(\vec N,\) направленная перпендикулярно наклонной плоскости, и сила трения \(\vec F_{тр},\) направленная по касательной к плоскости против движения бруска.
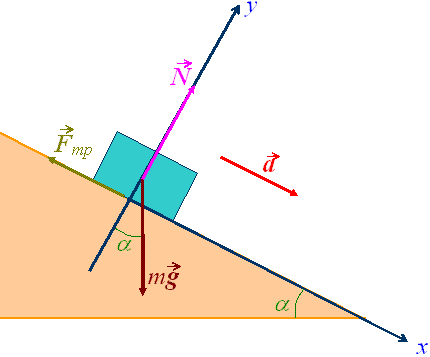
По второму закону Ньютона, равнодействующая этих сил равна произведению массы бруска на его ускорение$$\qquad \qquad \qquad \qquad \qquad m \vec g+\vec N+\vec F_{тр}=m \vec a. \qquad \qquad \qquad \qquad \qquad (1)$$ Проведём ось абсцисс вниз вдоль наклонной плоскости, а ось ординат перпендикулярно ей так, как это показано на рисунке. Запишем векторное уравнение (1) в проекциях на оси координат. Получим $$mg sin(\alpha)-F_{тр}=ma,$$$$-mg cos(\alpha)+N=0.$$ Из последниго уравнения получаем \(N=mg cos(\alpha).\) Сила трения, как это хорошо известно, равна \(F_{тр}=\mu N.\) Тогда$$mg sin(\alpha)-\mu mg sin(\alpha)=ma.$$Отсюда $$\mu=\frac{g sin(\alpha) - a}{g cos(\alpha)}.$$ Подставим данные в полученное выражение, находим искомое значение коэффициента трения в этой задаче по физике.$$\mu={9,81м/c^2sin(30^o)-1м/c^2)}{9,81м/c^2cos(30^o)}=0,46.$$ Ответ: \(\mu=0,46\).
Рассмотренные две задачи относятся к разделу физики, который называется динамика. Динамика, наряду со статикой, кинематикой и другими разделами, является частью механики. Механика очень большая, но не единственная часть физики. Физика состоит из различных разделов среди которых можно выделить следующие наиболее значимые разделы.
1. Механика, включающая кинематику, статику, динамику, релятивистскую механику
(общую теорию относительности, специальную теорию относительности) и прочее;
2. Молекулярная физика;
3. Термодинамика;
4. Статистическая физика;
5. Электродинамика, включающая электростатику, магнитостатику, электродинамику сплошных сред
и релятивистскую электродинамику;
6. Оптика, включающая геометрическую, волновую и квантовую оптики;
7. Атомная и ядерная физика, а также физика элементарных частиц;
8. Астрофизика;
9. Квантовая механика и квантовая физика;
10. Физика твёрдого тела.
И это далеко не все разделы физики, их перечисление можно ещё продолжить. Каждый из разделов физики делится в свою очередь на подразделы, и может рассматриваться как отдельная наука и содержать интересные задачи по физике.
Рассмотрим задачи по физике из какого-либо другого раздела, например, термодинамики.
Задача
Найти давление кислорода, находящегося в баллоне объёмом 100 литров и имеющего массу 100 грамм, при температуре 27oC.
Решение
Вначале переведём все величины в единицы системы СИ. Объём баллона \(V=0,1м^3.\) Масса газа \(m=0,1кг.\) Температура газа по абсолютной шкале \(T=273+27=300К.\)
По закону Менделеева - Клапейрона$$pV=\nu RT.$$Здесь \(\nu=m/\mu\) — количество вещества газа; \(\mu=0,032 кг/моль\) — молярная масса кислорода; \(R=8,31 Дж/(кг\cdot К)\) — универсальная газовая постоянная.
Исходя из сказанного, получим$$p=\frac{mRT}{\mu V}=\frac{0,1кг\cdot 8,31Дж/кг\cdot К \cdot 300К}{0,032кг/моль \cdot 0,1м^3}=77906,25Па.$$ Ответ: \(p=77,9 кПа.\)
Следующая задача по физике из раздела волновой оптики может показаться более сложной, чем предыдущие.
Задача
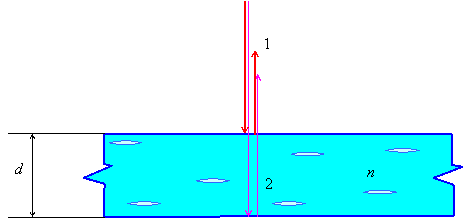
На тонкую пленку в направлении нормали к её поверхности падает монохроматический свет с длиной волны \(\lambda=500нм.\) Отраженный от неё свет максимально усилен вследствие интерференции. Определить минимальную толщину \(d_{min},\) если показатель преломления материала пленки \(n=1,4.\)

Решение
Оптическая разность хода световых лучей, возникающих при отражении монохроматического света от тонкой плёнки, равна
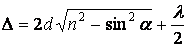
Здесь \(d\) — толщина плёнки, а \(\alpha\) — угол отклонения луча от нормали.
При \(\alpha=0^o\) оптическая разность хода

Условие максимального усиления света
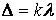
Подставляя \(\Delta,\) получим
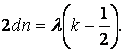
Отсюда, после преобразования, находим
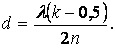
Минимальное значение \(d_{min}\) получится при \(k=1.\)$$d_{min}=\frac{\lambda}{4n}.$$ Подставим данные в формулу
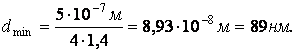
Проверим размерность.

Ответ: \(d_{min}=8,93\cdot10^{-8}м=89нм.\)
Задачи по физике могут относится к различным разделам науки. В конце представлена мультидисциплинарная задача по физике.
Задача
Какую массу льда, взятую при нуле градусов по Цельсию и нормальном давлении, можно растопить, а затем нагреть до температуры кипения и полностью испарить, с помощью энергии покоя одного грамма воды?
Решение
Ну, энергия покоя, она и есть энергия покоя, хоть одного грамма воды, хоть одного грамма золота. Энергия покоя вычисляется по формуле, изображённой на рисунке
Для одного грамма получаем \(E=10^{-3}кг\cdot(3\cdot 10^8м/с)^2=9\cdot10^{13}Дж.\)
С другой стороны, для плавления, нагревания и испарения льда массой \(m,\) при нормальных условиях потребуется тепло$$Q=m\lambda+mc\Delta t+mL.$$ Приравнивая это
тепло энергии покоя, найденной ранее, и выражая из полученного равенства массу льда, получим$$m=\frac E{\lambda+c\Delta t+L}=\frac{9\cdot10^{13}}{3,3\cdot10^5+4200\cdot100+2,3\cdot10^6=2,95\cdot10^7кг}=2,95\cdot10^4тонн.$$ Это масса воды нескольких олимпийских бассейнов.
Итак, мы рассмотрели некоторые задачи по физике. Большое количество задач по физике можно найти на нашем сайте. Если Вам нужно решение какой-либо задачи, которое вы не можете найти самостоятельно, присылайте нам условия и мы поможем решить её.
