

Задача по физике является одним из основных инструментов обучения на уроках физики. Не у всех одинаково легко получается освоить этот предмет. На этой странице мы рассмотрим на примерах, как решается стандартная задача по физике. В отличии от многих других предметов, физика не ограничивается набором фактов и знаний. Для её освоения недостаточно просто заучить наизусть часть материала. Требуется глубокое понимание взаимосвязей между отдельными частями этого предмета. Задача по физике и является тем инструментом, который позволяет глубже проникнуть в суть изучаемого материала. Рассмотрим несколько таких задач.
Задача по физике № 1
Сколько молекул находится в одном кубическом миллиметре кислорода при нормальном атмосферном давлении и температуре \(t=20^oC\)?
Дано: \(p=10^5Па\); \(V=1мм^3=10^{-9}м^3\); \(T=20^oC=293K\).
Решение.
Для решения этой задачи необходимо вспомнить, что кислород \(O_2\) в обычном состоянии является двухатомным газом с молярной массой \(\mu=0,032кг/моль.\) Нормальное атмосферное давление составляет \(p=100000Па (1 атмосфера).\) Далее вспомним формулу для количества вещества$$\nu=\frac m\mu=\frac N{N_A}.$$Здесь \(m\) — масса газа; \(N\) — число молекул газа; \(N_A=6,02\cdot10^{-23} моль^{-1}\) — число Авогадро, равное числу молекул в одном моле газа.
Из уравнения Менделеева-Клапейрона $$pV = \frac m{\mu}\cdot RT$$получаем выражение для молярной массы$$\nu=\frac{pV}{RT}.$$Здесь \(R=8,31 Дж/K\cdot моль\) — универсальная газовая постоянная.
Количество молекул$$N=\nu\cdot N_A=\frac{pVN_A}{RT}.$$Подставляя в полученную формулу данные, находим$$N={{10^5Па\cdot 10^{-9}м^3\cdot6,02\cdot10^{-23} моль^{-1}}\over{8,31Дж/(К\cdot моль)\cdot 293К}}=2,47\cdot10^{16}.$$ Ответ: \(N=2,47\cdot;10^{16}\).
Задачи по физике различаются по сложности и могут быть из различных разделов. Это ясно без слов. Можно было об этом не говорить. Рассмотрим простенькую задачу.
Задача по физике № 2
Найти центростремительное ускорение точки, движущейся по окружности радиуса \(25см\) со скорость \(50см/c.\)
Дано: \(R=25см=0,25м\) \(V=50см/c=0,5м/c.\) Найти: \(a_ц=?\)
Решение.
Центростремительное ускорение, возникающее при движении точки по окружности и направленное к центру этой окружности, вычисляется по формуле:$$a_ц=\frac{V^2}R.$$
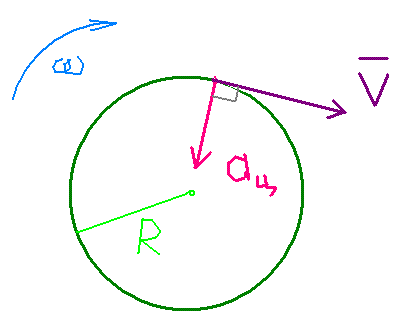
Подставляя в последнее выражение данные, получим$$a_ц=\frac{(0,5м/c)^2}{0,25м}=1м/с^2.$$ Ответ: \(a_ц=1 м/с^2\).
Следующая задача по физике является немного более сложной, чем предыдущая. Хотя, по сути, также является довольно простой.
Задача по физике № 3
С какой высоты должен падать град, чтобы полностью испариться при падении? Температуру льдинок принять равной \(0^oC.\) Считать, что потери энергии не происходит и вся энергия расходуется только на нагревания градинок. Сопротивление воздуха не учитывать. Удельная теплоёмкость воды \(c=4200Дж/(кг\cdot^oC).\) Удельная теплота плавления льда \(\lambda=3,3\cdot;10^5Дж/кг.\) Удельная теплота парообразования воды \(r=2,3\cdot10^6Дж/кг.\)
Решение.
Эта задача на применение закона сохранения энергии. В рассматриваемом примере гравитационная потенциальная энергия шариков града сначала превращается в кинетическую энергию движения этих шариков, а затем преобразуется в тепло. Тепло расходуется на плавление льда, последующее нагревание образовавшейся воды до температуры кипения и её испарение. Рассмотрим произвольную льдинку массой \(m\), начинающую своё падение с высоты \(h\). Потенциальная энергия этой льдинки$$E_п=mgh.$$ Тепло, требуемое для плавления льда, находим по формуле \(Q_1=m\lambda.\) Тепло, необходимое для нагревания образовавшейся воды и доведения её до кипения при температуре \(100^oC,\) равно \(Q_2=mс(t_{кипения}-0).\) Тепло, необходимое для испарения образовавшейся воды, находим по формуле \(Q_3=mr.\) Таким образом, общее тепло, идущее на плавление, нагревание и испарение, равно$$Q=Q_1+Q_2+Q_3=m\lambda+mс(t_{кипения}-0)+mr.$$ По закону сохранения энергии это тепло равно потенциальной энергии льдинок в начале падения, то есть \(Q=E_п,\) или$$m\lambda+mс(t_{кипения}-0)+mr=mgh.$$ Разделим последнее уравнение на \(mg.\) Получим$$h=\frac{\lambda+сt_{кипения}+r}g.$$ Подставляя данные, находим$$h=\frac{3,3\cdot 10^5Дж/кг+4200Дж/(кг\cdot^oC)\cdot 100^oC+2,3\cdot10^6Дж/кг}{9,81м/c^2}=310907м=311км.$$ Ответ: \(h=311км\).
Задача по физике № 4
Под действием силы тяги \(6кН\) автомобиль совершает перемещение \(54м\) в направлении действия силы тяги. Какую работу совершает сила тяги? Какую скорость будет иметь автомобиль в конце этого перемещения, если его масса равна \(40тонн?\)
Дано: \(F=6кН=6000Н;\) \(s=54м;\) \(m=40т=40000кг.\) Найти: \(A, v.\)
Решение.
Работа равна произведению силы на перемещение.$$A=Fs=6000Н\cdot54м=324000Дж=324кДж.$$ По второму закону Ньютона ускорение автомобиля равно$$a=\frac Fm.$$ При равноускоренном движении перемещение и скорость определяются формулами$$s=\frac{at^2}2, \qquad v = at.$$Отсюда$$t=\sqrt{\frac{2s}a}, \qquad v=\sqrt{2sa}.$$ Подставляя в последнее уравнение выражение для ускорения, а затем производя вычисления, находим$$v=\sqrt{2sa}=\sqrt{\frac{2sF}m}=\sqrt{\frac{2\cdot54м\cdot6000Н}{40000кг}}=4,02\frac мс.$$ Ответ: \(A=324кДж, \; v=4,02м/с.\)
Задача по физике № 5
На некоей экзопланете математический маятник длиной \(1,2м\) совершает \(100\) гармонических колебаний за \(3\) минуты. Найти ускорение свободного падения на поверхности этой планеты и первую космическую скорость для неё, если известно, что её радиус равен \(8500км.\)
Дано: \(l=1,2м\); \(N=100;\) \(t=3мин=180с.\) \(R=8500км=8,5\cdot10^6м.\) Найти: \(g, \, v=?\)
Решение.
Период колебаний маятника есть время, за которое совершается одно колебание маятника. Поэтому

С другой стороны, период колебаний математического маятника определяется формулой
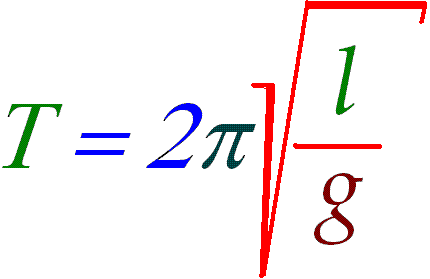
Приравнивая периоды, получим
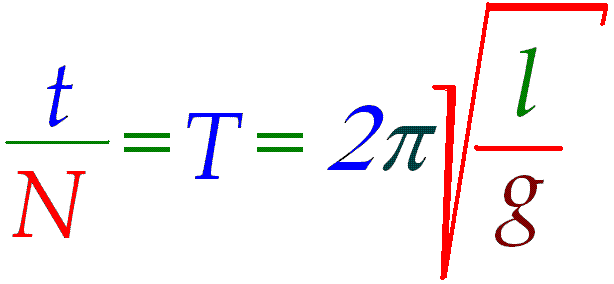
Отсюда
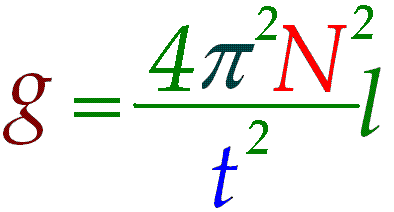
Подставляя данные в последнюю формулу, находим для ускорения свободного падения на поверхности экзопланеты \(g=14,606м/с^2.\)
Первая космическая скорость на планете определяется формулой
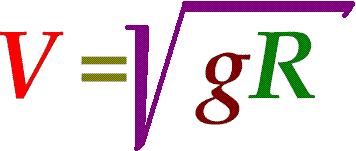
Таким образом \(v=11142м/с=11,14км/с.\) Почти как на Земле. Для Земли первая космическая скорость равна \(7,9км/c.\)
Ответ: \(g=14,606м/с^2,\) \(V=11,142м/с^2.\)
Задача по физике № 6
Некоторый газ находится в закрытом сосуде при температуре \(20^oC\) и давлении \(100000Па.\) Сосуд нагревают до \(80^oC.\) Как при этом изменяется давление газа в сосуде?
Дано: \(T_1=20^oC=20+273=293K;\) \(T_2=80^oC=80+273=353K;\) \(p_1=100000Па.\) Найти: \(p_2=?\)
Решение.
Так как газ находится в закрытом сосуде, то процесс изохорный. Для изохорного процесса, по закону Шарля $$\frac{p_2}{p_1}=\frac{T_2}{T_1}.$$Отсюда$$p_2=p_1\cdot\frac{T_2}{T_1}=100000Па\cdot\frac{353К}{293К}=120477Па=120кПа.$$ Ответ: \(p_2=120,5кПа.\)
Следующая задача по физике относится к разделу "Электростатика". Для решения этой задачи необходимо знать закон Ома и понимать как сопротивление цепи зависит от типа соединения. На рисунке представлены два способа соединения резисторов. При последовательном соединении сопротивления резисторов складываются, а при параллельном соединении складываются обратные величины сопротивлений.
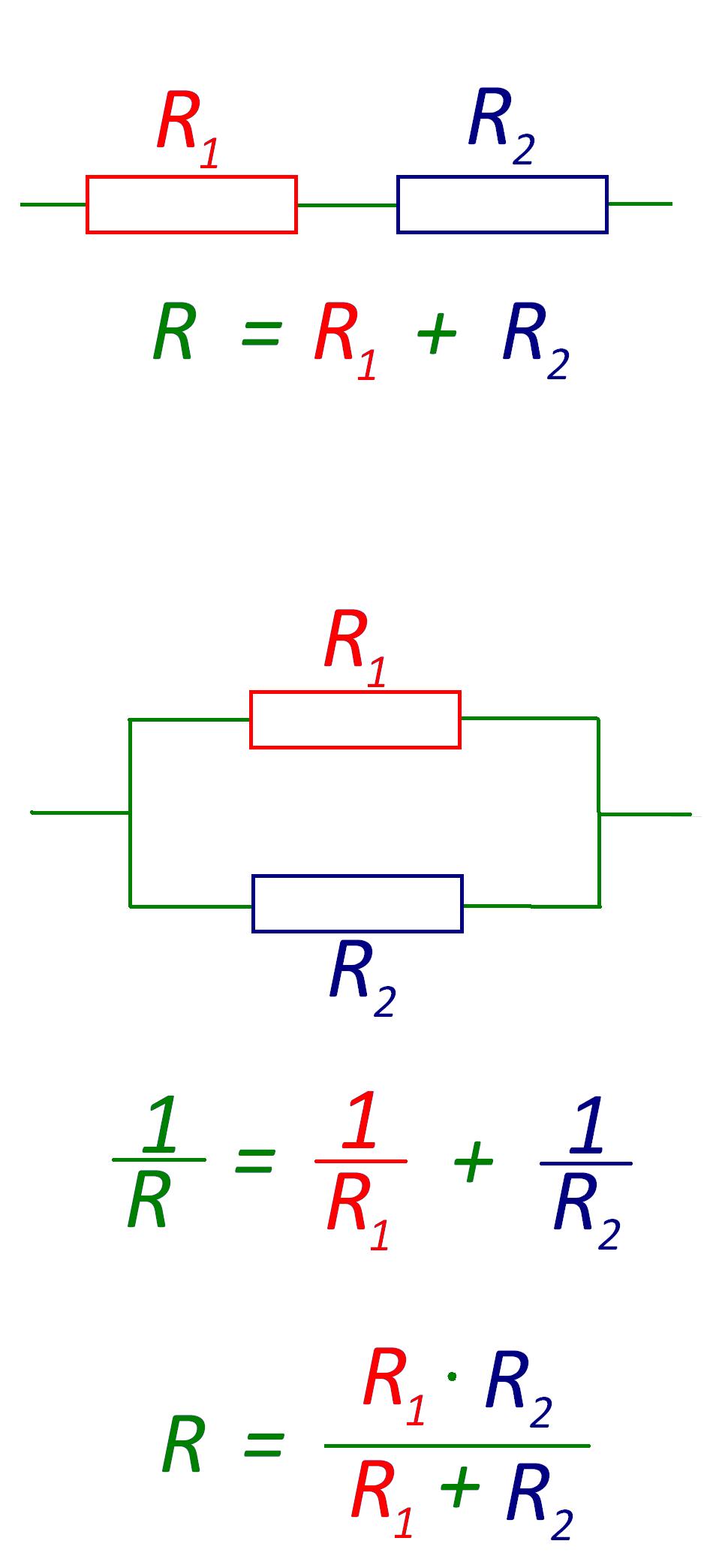
Закон Ома устанавливает пропорциональную взаимосвязь между напряжением и силой тока на участке цепи. При этом коэффициентом пропорциональности является сопротивление участка цепи. То есть
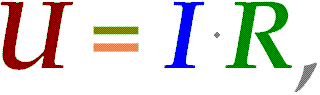
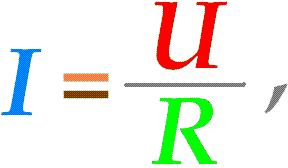
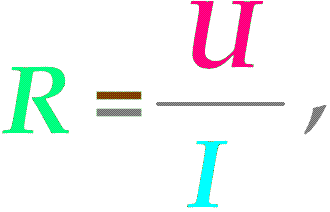
как-то так.
Задача по физике № 7
Два сопротивления \(200Ом\) и \(300Ом\) соединены сначала последовательно, а потом параллельно. На участок цепи, созданный таким образом, подаётся напряжение \(50\)
Дано: \(R_1=200Ом;\) \(R_2=300Ом;\) \(U=50В;\) Найти: \(I_I=?\) \(I_{II}=?\)
Решение.
Сопротивление участка при последовательном соединении:$$R_I=R_1+R_2=200Ом+300Ом=500Ом.$$ По закону Ома:$$I_I=\frac U{R_I}=\frac {50В}{500Ом}=0,1А.$$ Сопротивление участка при параллельном соединении: $$R_{II}=\frac{R_1\cdot R_2}{R_1+R_2}=\frac{200Ом \cdot 300Ом}{200Ом+300Ом}=120Ом.$$ По закону Ома:$$I_{II}=\frac U{R_{II}}=\frac{50В}{120Ом}=0,417А.$$ При параллельном соединении сила тока больше, чем при последовательном.
Ответ: \(I_I=0,1А,\) \(I_{II}=0,417 А.\)
Задача по физике № 8
Какой заряд протекает через поперечное сечение проводника сопротивлением \(2,2 кОм\) за \(10\) минут, если проводник находится под напряжением \(300 кВ?\) Какое тепло выделится при прохождении тока через проводник?
Дано: \(R=2,2кОм=2200Ом;\) \(U=300кВ=3\cdot10^5В;\) \(t=10мин=600с.\) Найти: \(q=?\) \(Q=?\)
Решение.
По закону Ома
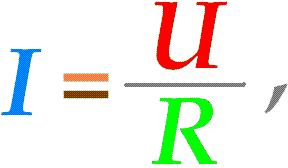
то есть $$I=\frac{300000В}{2200Ом}=136,364А.$$ Заряд, протекающий через поперечное сечение проводника, равен$$q=It=136,364А\cdot600c=81818Кл=81,82кКл.$$ По закону Джоуля-Ленца, тепло, выделяющееся в проводнике, определяется формулой
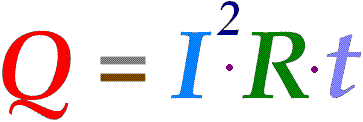
Подставляя данные и производя вычисления, получим:$$Q=2,455\cdot10^10Дж=24,5Гдж.$$ Ответ: \(q=81,82кКл,\) \(Q=24,5ГДж.\)
Как нетрудно догадаться, для учителей и преподавателей технических образовательных учреждений задача по физике является не только важнейшим инструментом обучения школьников и студентов, значимым элементом контрольных, зачётных, экзаменационных работ и домашних заданий, но и мощным средством стимулирования учащихся к познанию и творческому переосмыслению явлений природы на занятиях физики.
Также и на нашем сайте в полном соответствии с требованиями времени, потребностями учащихся и нашим искренним желанием, задача по физике занимает весьма значительное место.
