ИСТОРИЯ МАТЕМАТИКИ: ГЕОМЕТРИЧЕСКАЯ АЛГЕБРА

        От Пифагора до Гиппазия

        Первой научной школой, предложившей свой вариант математического плана строения Вселенной, были пифагорейцы. Школа пифагорейцев существовала в Древней Греции около 585–500 годов до нашей эры и возглавлялась Пифагором Самосским. Пифагорейцы видели сущность явлений в числе и числовых отношениях. Отсюда и основной тезис учения пифагорейцев: “Все вещи суть числа”.

        Привычное нам понятие числа возникло в результате абстрагирования. Ранним пифагорейцам такая абстракция была чужда. Для них числа были точками или частицами, расположенными на плоскости (поверхности Земли). Рассматривая треугольные, квадратные и т.д. числа, называемые фигурными, пифагорейцы имели в виду наборы точек, камешков или других мелких предметов, расположенных в форме треугольников, квадратов и других фигур (рис.1, 2).

        Во всех явлениях природы пифагорейцы искали числовые соотношения и взаимосвязи. Их поражал тот факт, что совершенно различные явления, будь то музыкальные созвучия или движения планет, подчиняются числовым соотношениям.

        После того как пифагорейцы связали астрономию и музыку с арифметикой и геометрией, все четыре дисциплины стали считаться математическими. Эта точка зрения оставалась господствующей вплоть до средневековья.

Рисунок 1. Треугольные числа: 1, 3, 6.

Рисунок 2. Квадратные числа: 1, 4, 9.

        Пифагорейцы считали, что все вещи в природе, как и музыкальные ноты, соразмерны, то есть их числовые характеристики соотносятся друг к другу как целые числа. Отношения целых чисел представляют собой рациональные числа. Считалось, что длины любых двух отрезков относятся как целые числа. Во времена пифагорейцев под целыми числами понимались именно натуральные числа. Когда же обнаружилось, что отношение гипотенузы прямоугольного треугольника к катету не является отношением целых чисел, это удивило и весьма обеспокоило пифагорейцев. Отношения, представимые в идее целых чисел, они называли соизмеримыми, а отношения, непредставимые в идее целых чисел несоизмеримыми. Открытие несоизмеримых отношений легенда приписывает Гиппазию, жившему в V веке до нашей эры в местечке Метапонт. Гиппазий совершил своё открытие, когда он вместе с коллегами находился в открытом море. Товарищи обвинили Гиппазия, в ереси, привнесшей в мироздание элемент, противоречащий пифагорейскому учению, и выбросили его за борт. Согласно Аристотелю, Гиппазий должен был рассуждать следующим образом. Действительно, пусть $$\sqrt2=\frac ab,$$где \(a\) и \(b\) — взаимно-простые целые числа (предполагается, что общие множители уже сокращены). Тогда \(a=\sqrt2 b\) и \(a^2=2b^2\), то есть \(a^2\) является чётным числом, а, следовательно, чётным числом является и \(a\), так как квадрат нечётного числа есть число нечётное. Таким образом, \(a=2c\). Но, так как \(a^2\) и \(b^2\) взаимно-простые числа, то \(b^2\) есть нечётное число. С другой стороны, так как \(a^2=2b^2\) b \(a^2=(2c)^2=4c^2\), то есть \(4c^2=2b^2\) и \(b^2=2c^2\), получается, что число \(b^2\) есть чётное число. Полученное противоречие доказывает, несоизмеримость числа \(\sqrt2\) (\(\sqrt2\) — длина гипотенузы равнобедренного прямоугольного треугольника с катетом \(1\) или диагональ квадрата со стороной \(1\)). В современной терминологии несоизмеримые числа, такие как \(\sqrt2\) или \(\sqrt3\), называют иррациональными.



        Геометрическая алгебра

        Открытие иррациональных чисел повергло в шок пифагорейцев, и поставило задачу, ставшую центральной для греческой математики. Решение этой задачи предложил Евдокс, бывший учеником Платона. По Евдоксу понятие величины надлежит трактовать геометрически как длины отрезков, углы, площади и объёмы. Именно так Евклид формулирует легендарную теорему Пифагора: квадрат, построенный на гипотенузе прямоугольного треугольника, равен сумме квадратов катетов (рис. 3). Под квадратом величины Евклид понимает площадь квадрата, построенного на стороне заданной длины.

        Обращение за помощью к геометрии вполне оправдано. Если числа \(1\) и \(\sqrt2\) рассматривать как длины отрезков, то принципиальная разница между ним сглаживается и даже порой исчезает. Греки классического периода решали алгебраические уравнения геометрически, представляя их корни в виде отрезков, тем самым, избегая необходимости обращаться к иррациональным числам. Это направление в развитие математики получило название геометрической алгебры. По сути, отказавшись от исследования природы иррациональности и свойств иррациональных чисел, греки начали строить математику на основе геометрии. В частности, при построении алгебры, её операции определялись непосредственно для геометрических величин, а теоремы доказывались геометрическими построениями.

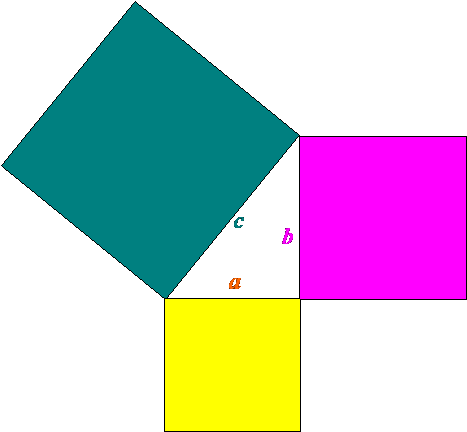
Рисунок 3. Геометрическое изображение теоремы Пифагора.

        Построение алгебры на основе геометрии позволило впервые обосновывать многие теоремы алгебры в общем виде. Однако геометризация алгебры имела и весьма существенный побочный эффект, связанный с трудоёмкостью доказательств. Геометризация доказательств привела к сковыванию алгебры и ограничению её вычислительных и прикладных возможностей.

        Начав построение геометрической алгебры, греки стали применять геометрический язык в теории чисел. Числа теперь изображались не точками, расположенными в виде правильных фигур, а представлялись отрезками. Некий отрезок принимался за единицу, а отрезок, полученный из данного, многократным повторением, принимался за целое число.

        Наиболее последовательно и полно геометрическая алгебра изложена во второй книге «Начал» Евклида, а также трудах, других греческих математиков александрийского периода, в частности, Архимеда и Аполлония.

        Основные положения геометрической алгебры сводятся к следующему:
        1) алгебраические переменные, как и произвольные числа, представляются отрезкам;
        2) сумма чисел или алгебраических переменных представляется в виде отрезка, составленного из слагаемых (рис. 4);
       3) произведение двух чисел или алгебраических переменных представляется в виде прямоугольника со сторонами, которые представляют собой отрезки, соответствующие сомножителям (рис. 5). Произведение трёх переменных \(a, b\) и \(c\) есть прямоугольный параллелепипед со сторонами, соответствующими сомножителям \(a, b\) и \(c\) (рис. 6).

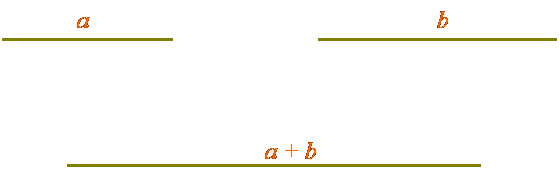
Рисунок 4. Сложение а и b.

        Поскольку, греческая геометрия, как и в целом представления греков о природе и мироздании ограничивались тремя измерениями, произведение более чем трёх переменных в геометрической алгебре не рассматривались, как лишённые смысла.

        Так как сложением отрезков происходит посредством приставления одного к другому, то вычитание, очевидно, осуществляется путём укорочения большего отрезка на часть, равную меньшему отрезку. Поскольку греки не рассматривали отрицательные числа, то операция вычитания возможна только тогда, когда из большего вычитается меньшее.

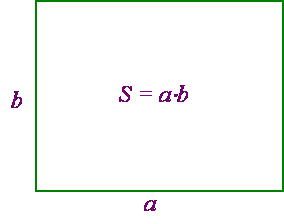
Рисунок 5. Произведение чисел \(a\) и \(b\) есть площадь прямоугольника со сторонами \(a\) и \(b\).

        Вычисления, производимые в геометрической алгебре, носили пошаговый характер. Не рассматривались произведения прямоугольников или сложение прямоугольников с отрезками или параллелепипедами.

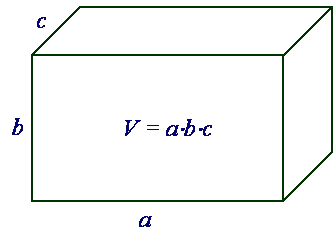
Рисунок 6. Произведение трёх чисел \(a, b\) и \(c\) есть объём параллелепипеда со сторонами \(a, b\) и \(c\).

        Геометрическая наглядность позволила легко обосновать свойства основных операций над числами: сложения и умножения. Например, коммутативность сложения легко следует из того факта, что длина составного отрезка, одна и та же с какой стороны на него не посмотри, то есть $$a+b=b+a.$$         Коммутативность умножения обосновывается так же наглядно, поворотом соответствующего прямоугольника, то есть $$a\cdot b=b \cdot a.$$         Ассоциативность сложения наглядно следует из того факта, что в каком порядке не прикладывай отрезки друг к другу, длина составного отрезка будет одинаковой, то есть $$(a+b)+с=a+(b+c).$$         Ассоциативность умножения наглядно визуализируется поворотом прямоугольного параллелепипеда, то есть $$(a\cdot b)\cdot с=a \cdot(b\cdot c).$$         Во второй книге «Начал» Евклида геометрически обосновывается дистрибутивность сложения по отношению к умножению (рис. 7).

Рисунок 7. Геометрическое представление закона дистрибутивности
\((a+b)\cdot c=a\cdot c+b\cdot c\).

        Как видно из этих примеров, наглядность является серьёзным преимуществом геометрической алгебры. Но гораздо более важным преимуществом использования геометрических методов в алгебре явилось то, что обоснования и доказательства тождеств не зависят от того, являются ли используемые величины соизмеримыми или несоизмеримыми и независимы от конкретных величин.

        Методы геометрической алгебры позволили доказать многие алгебраические тождества. При этом общее доказательство было сделано впервые в истории. Например, установлено известное тождество квадрата суммы как суммы квадратов и удвоенного произведения: $$(a+b)^2=a^2+b^2+2\cdot a\cdot b.$$   Геометрическое обоснование этого известнейшего алгебраического тождества представлено на рисунке 8.

        Аналогично обосновываются другие известные тождества: $$(a–b)^2=a^2+b^2-2\cdot a\cdot b.$$$$(a–b)\cdot(a+b)=a^2–b^2.$$         Упомянутые тождества устанавливались для величин двух измерений. Для трёх измерений пришлось бы использовать пространственные фигуры, параллелепипеды. Визуализация кубических тождеств значительно сложнее, так как требует незаурядного пространственного воображения.

        Как уже упоминалось выше, произведения четырех и более величин не использовались греческими математиками как не имеющие смысла и не позволяющие визуализации в рамках трехмерного физического пространства.

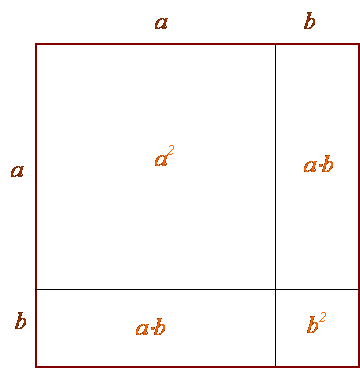
Рисунок 8. Геометрическое представление алгебраического тождества квадрата суммы.

        Античная геометрия состояла как из планиметрии, так и стереометрии, которая содержала сферическую тригонометрию и теорию конических сечений, используемые в астрономии. Однако геометрическая алгебра в основном опиралась на планиметрию и обосновывала её. В значительной степени планиметрия античности это геометрия построений с помощью циркуля и линейки. В этой связи, наибольшее применение геометрическая алгебра нашла в вопросах исследования квадратичных форм и тождеств, а также при решении квадратных уравнений.

        Неразрешённые задачи

        В античности греческие математики решали задачи, сводящиеся к квадратным уравнениям, с помощью циркуля и линейки. Как было установлено позднее, решение задач, построением с помощью циркуля и линейки, сводится алгебраически к решению квадратных уравнений. В таких построениях используются следующие шаги: проведение прямой через две точки; нахождение точки пересечения двух прямых; нахождение точек пересечения прямой и окружности или двух окружностей. Первые два шага, как это следует координатного метода аналитической геометрии Р. Декарта, алгебраически эквивалентны решению линейных уравнений. Третий шаг эквивалентен решению квадратного уравнения. Из координатного метода и аналитической геометрии Декарта следует, что уравнения степени, большей двух, не могут быть решены построениями с помощью циркуля и линейки.

        Ограниченность возможностей геометрической алгебры античные математики ощутили уже в V веке до нашей эры, когда были поставлены три классические задачи. Эти задачи разрешились уже другими средствами лишь в XIX веке. К таковым задачам относятся следующие задачи: задача об удвоение куба, задача о трисекция угла и задача о квадратуре круга. Классическая геометрическая алгебра оказалась бессильной перед этими задачами, и для их решения понадобилось создание новых методов.

        Задача об удвоении куба формулируется следующим образом. Построить куб объемом, превосходящим заданный куб, в два раза. В современных символьных выражениях эта решение задачи сводится к кубическому уравнению \(x^3=2\cdot a^3\). Однако с помощью циркуля и линейки эта задача не разрешалась.

        В задаче трисекции угла требуется разделить заданный угол на три равные части, также используя только циркуль и линейку. Античные математики не свели эту задачу к кубическому уравнению. Однако с помощью тригонометрических методов её можно привести к решению уравнения \(3\cdot x–4x^3=a\). Это удалось сделать математикам Арабского Халифата.

        Задача о квадратуре круга формулируется так. Построить квадрат, площадь которого равновелика площади данного круга.

        Ученые древности убедились в неразрешимости (в общем случае) задач, эквивалентных кубическим уравнениям. С помощью циркуля и линейки эти задачи не решаются. Леонардо из Пизы сделал первую попытку доказательства неразрешимости кубического уравнения с помощью квадратных иррациональностей. При этом он исследовал частный случай кубического уравнения$$x^3+2\cdot x^2+10\cdot x=20.$$         Великий французский мыслитель, математик и философ Рене Декарт, позднее сформулировал положение, согласно которому, корни кубического уравнения с рациональными коэффициентами могут быть построены с помощью циркуля и линейки только лишь в том случае, когда это уравнение приводимо, то есть имеет не менее одного рационального корня. Аналогичный критерий был найден Декартом и для уравнений четвертой степени.

        От Евклида и вплоть до Декарта геометрическая алгебра преследует своей целью сведение алгебраически утверждений к геометрическим, и таким образом обоснование алгебры свести к обоснованию геометрии, которая на протяжении многих столетий считалась образом логической строгости. Рене Декарт повернул этот процесс вспять, применив изобретённый им координатный метод к геометрии, создав, таким образом, аналитическую геометрию и заложив основы алгебраической геометрии. Однако геометрическая алгебра античной Греции может по праву считаться прообразом и первым шагом на пути к алгебраической геометрии.

Литературные источники

        1. Клайн М. Математика. Утрата определённости. — М.: Мир, 1984.

        2. Ван дер Варден Б. Пифагорейское учение о гармонии. — М.: Физматгиз., 1979.