Задача 11. Найти решение задачи Коши.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        11.17. Найти решение задачи Коши

y″ = 8·sin³y·cosy,     y(1) = π/2,     y′(1) = 2.

Решение

        Это дифференциальное уравнение, допускающее понижение порядка. Порядок дифференциального уравнения может быть понижен при помощи замены

y′ = p(y).

        Тогда

y″ = p·p′ .

        После подстановки, дифференциальное уравнение запишется

p·p′ = 8sin³ycosy .

        Это дифференциальное уравнение с разделяющимися переменными. Разделим переменные в полученном дифференциальном уравнении

p·dp = 8sin³ycosy dy.

        Интегрируем последнее дифференциальное уравнение.

∫p·dp = ∫8sin³ycosy dy.

        После интегрирования, получим

p² = 4sin⁴y + С,

        Подставим начальные условия. При y = π/2, p = y′ = 2. Тогда

4 = 4sin⁴(π/2) + С,

        или C = 0.

        В результате, после подстановки C в найденное решение и извлечения корня с обеих сторон, получаем

y′ = p = 2sin²y.

        Получили дифференциальное уравнение первого порядка с разделяющимися переменными. Разделим переменные

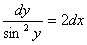
        и проинтегрируем

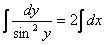
        В результате получим

ctgy = −2x + C₁.

        Подставим начальные условия. При y = π/2, x = 1. Тогда

ctg(π/2) = −2 + C₁,

        или C₁ = 2.

        Искомое решение задачи Коши для исходного дифференциального уравнения второго порядка принимает вид

ctgy = 2−2x,

        или

y = arctg(2−2x).

        Ответ: Решение задачи Коши    y = arctg(2−2x).