Задача 6. Найти решение задачи Коши..

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

        6.17. Найти решение задачи Коши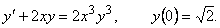    

Решение

        Это дифференциальное уравнение Бернулли. Разделим обе части этого уравнения на y ³. Получим

y ^-3y′ + 2xy ^-2 = 2x³.

        Сделаем замену   z = y^-2,   тогда

z′ = -2y^-3y′,

        или

y^-3y′ = -0,5z′.

        После подстановки в уравнение получим линейное дифференциальное уравнение

-0,5z′+2xz = 2x³

        или

z′-4xz = -4x³.

        Будем решать его методом Бернулли. Для этого сделаем замену

z = uv, z′ = u′v + uv′ .

        Тогда дифференциальное уравнение запишется в виде

u′v + uv′ – 4xuv = -4x³ .

        или в виде

(u′ – 4xu)v + uv′ = -4x³.

        Примем, что

u′ – 4xu = 0.

        тогда

uv′ = -4x³.

        Разделяя переменные, запишем дифференциальное уравнение в виде двух уравнений с разделяющимися переменными

        Интегрируем полученные дифференциальные уравнения

        Тогда

        Интегрируем по частям (Используем формулу интегрирования по частям).

        В последнем интеграле сделаем замену   t = -2x²,   и   dt = -4xdx.

        Тогда

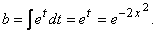
        Следовательно,

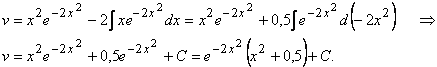
        Тогда

        Но

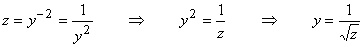
        Следовательно, общее решение дифференциального уравнения Бернулли имеет вид

        Для определения неизвестной постоянной С, используем начальное условие

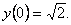
        Тогда

        Отсюда С=0, и решение задачи Коши принимает вид

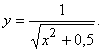
        Ответ: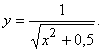    

        Сделаем проверку. Найдём производную полученного решения.

        Подставим в исходное уравнение

        Получили тождество. Проверим начальное условие

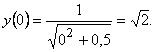
        Верно.

        Таким образом, решение задачи Коши найдено верно.