Графики

Исследование функции проводится в соответствии с планом полного исследования функции. Посмотрите образец такого исследования с построением графика.

Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

7.3. Провести полное исследование функции и построить её график$$y(x)=\frac2{x^2+2x}.$$

Решение.

1) Область определения: $x^2+2x\neq0$ или $(x+2)x\neq0,$ то есть $x\neq0$ и $x\neq-2.$

Таким образом: $x\in(-\infty; \, -2)\cup(-2; \, 0)\cup(0; \, +\infty).$

2) Точек пересечения с осью Ox нет. Действительно, уравнение $\frac2{x^2+2x}=0$ не имеет решений. Точек пересечения с осью Oy нет, так как $x\neq0.$

3) Функция ни чётная, ни нечётная. Симметрии относительно оси ординат нет. Симметрии относительно начала координат тоже нет. Так как$$y(-x)=\frac2{(-x)^2+2(-x)}=\frac2{x^2-2x}.$$Видим, что $y(-x)\neq-y(x)$ и $y(-x)\neq y(x).$

4) Функция непрерывна в области определения $x\in(-\infty; \, -2)\cup(-2; \, 0)\cup(0; \, +\infty).$$$\lim_{x\to-2-0}y(x)=\lim_{x\to-2-0}\frac2{x^2+2x}=+\infty; \qquad \lim_{x\to-2+0}y(x)=\lim_{x\to-2+0}\frac2{x^2+2x}=-\infty.$$Следовательно, точка $x=-2$ является точкой разрыва второго рода (бесконечный разрыв).$$\lim_{x\to-0}y(x)=\lim_{x\to-0}\frac2{x^2+2x}=-\infty; \qquad \lim_{x\to+0}y(x)=\lim_{x\to+0}\frac2{x^2+2x}=+\infty.$$Следовательно, точка $x=0$ является точкой разрыва второго рода (бесконечный разрыв).

5) Вертикальные асимптоты: $x=-2; \; x=0.$ Найдём наклонную асимптоту $y=kx+b.$ Здесь$$\lim_{x\to\infty}\frac{y(x)}x=\lim_{x\to\infty}\frac2{x^3+2x^2}=0; \qquad \lim_{x\to\infty}(y(x)-kx)=\lim_{x\to\infty}\left(\frac2{x^2+2x}-0\right)=0.$$Следовательно, имеем горизонтальную асимптоту: $y=0.$ Наклонных асимптот нет.

6) Найдём первую производную. Первая производная:$$y'(x)=\left(\frac2{x^2+2x}\right)'=2\frac{-(x^2+2x)'}{(x^2+2x)^2}=-\frac{4(x+1)}{(x^2+2x)^2}.$$ Cтационарные точки — это точки, в которых производная равна нулю, то есть$$y'(x)=-\frac{4(x+1)}{(x^2+2x)^2}=0.$$Тогда $x+1=0,$ и $x=-1.$

7) Найдём вторую производную. Вторая производная равна $$y''(x)=\left(-\frac{4(x+1)}{(x^2+2x)^2}\right)'=-4\frac{(x+1)'(x^2+2x)^2-(x+1)\left((x^2+2x)^2\right)'}{\left((x^2+2x)^2\right)^2}=$$$$=-4\frac{(x^2+2x)^2-(x+1)\left(2(x^2+2x)(2x+2)\right)}{\left(x^2+2x\right)^4}=-4\frac{(x^2+2x)\left((x^2+2x)-4(x+1)^2\right)}{\left(x^2+2x\right)^4}=$$$$=-4\frac{x^2+2x-4x^2-8x-4}{\left(x^2+2x\right)^3}=\frac{4(3x^2+6x+4)}{\left(x^2+2x\right)^3}.$$ Найдём точки перегиба графика функции, в которых вторая производная обращается в ноль. То есть$$y''(x)=\frac{4(3x^2+6x+4)}{\left(x^2+2x\right)^3}=0 \quad или \quad 3x^2+6x+4=0.$$Решаем полученное квадратное уравнение.$$D=b^2-4ac=6^2-4\cdot3\cdot4=-12\lt0.$$Следовательно, решений нет. Тогда тестовые интервалы:

Результаты исследования функции занесем в таблицу.

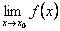
Функция имеет максимум в точке $x=-1$, при этом $y_{max}=y(-1)=-2.$

8) Данные таблицы нанесем на координатную плоскость. Используя результаты исследования функции, построим ее график.