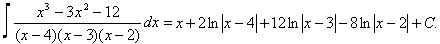Задача 5. Найти неопределённые интегралы.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

Решение

---

        5.10. Найти неопределённый интеграл    .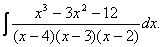

Решение.

        Разделим подынтегральную дробь. Получим

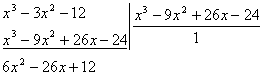
        Искомый неопределённый интеграл запишется

.

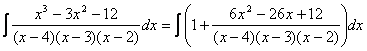        Разложим дробь 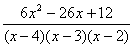    на простейшие дроби

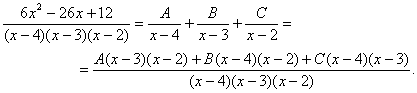
        Отсюда

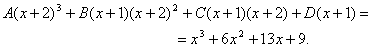
        Подставим значения аргумента так, чтобы сократить все слагаемые в числителе, кроме того, который содержит 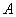. При   ,  
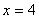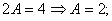
        Подставим значения аргумента так, чтобы сократить все слагаемые в числителе, кроме того, который содержит 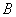. При   ,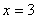  
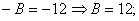
        Подставим значения аргумента так, чтобы сократить все слагаемые в числителе, кроме того, который содержит 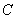. При ,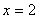  
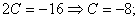
        Следовательно, неопределённый интеграл запишется в виде

.

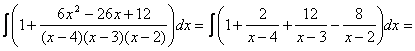
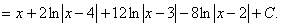        Ответ:    

---