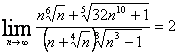Задача 3. Вычислить пределы числовых последовательностей.

        Введите номер своего варианта или решите задачу по образцу, приведённому ниже.

Решение

---

        3.31. Вычислить предел числовой последовательности

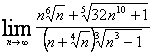
Решение.

        Для того, чтобы вычислить предел числовой последовательности вынесем множители за скобки

        Используем известное свойство 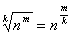. Тогда 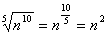и .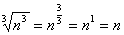

        Предел последовательности запишется

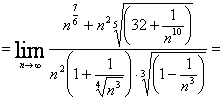
        Вынесем в последнем выражении в пределе n² за скобки в числителе и знаменателе, а потом сократим

        Предел числовой последовательности обладает следующими свойствами

,
,
,
,

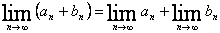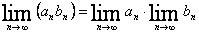        То есть предел последовательности, суммы двух числовых последовательностей, равен сумме пределов этих последовательностей. Предел разности двух последовательностей равен разности их пределов. Предел частного последовательностей равен частному их пределов.
        Тогда для искомого передела можем записать

.

        Так как     .

       Ответ: Предел числовой последовательности равен

---