Задача 12. Исследовать кривую второго порядка и построить её.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
Алгебраическая линия второго порядка или кривая второго порядка — это линия, координаты точек которой удовлетворяют уравнению$$Ax^2+Bxy+Cy^2+Dx+Ey+F=0.$$ Преобразованием координат уравнение кривой второго порядка можно привести к каноническому виду. Существует девять кривых второго порядка, имеющих следующие канонические уравнения.
Эллипс.
Каноническое уравнение эллипса: \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.\)
Гипербола.
Каноническое уравнение гиперболы: \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.\)
Парабола.
Каноническое уравнение параболы: \(y^2=2px.\)
Пара пересекающихся прямых. \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=0.\)
Пара параллельных прямых. \(x^2-a^2=0.\)
Пара совпадающих прямых. \(x^2=0.\)
Мнимый эллипс. \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=-1.\)
Пара пересекающихся мнимых прямых. \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=0.\)
Пара параллельных мнимых прямых. \(x^2+a^2=0.\)
Задача 12. Исследовать кривую второго порядка \(17x^2+12xy+8y^2-20=0\) и построить её.
Решение.
Группа старших членов данного уравнения образует квадратичную форму \(\Phi(x, y)=17x^2+12xy+8y^2.\) Её матрица$$A=\begin{pmatrix}17&6\\6&8\end{pmatrix}.$$ Составим характеристическое уравнение \(det((a-\lambda E)=0,\) или$$\begin{vmatrix}17-\lambda&6\\6&8-\lambda\end{vmatrix}=0.$$ Расписывая определитель, получим \((17-\lambda)\cdot(8-\lambda)-36=0.\) Раскрывая скобки, получим квадратное уравнение \(\lambda^2-25\lambda+100=0.\) Дискриминант этого квадратного уравнения положителен$$D=25^2-4\cdot1\cdot100=625-400=225=15^2$$и корни$$\lambda_1=\frac{-(-25)-\sqrt D}{2\cdot1}=\frac{25-15}2=\frac{10}2=5, \quad \lambda_2=\frac{-(-25)+\sqrt D}{2\cdot1}=\frac{25+15}2=\frac{40}2=20.$$ Следовательно, квадратичная форма \(\Phi(x, y)=17x^2+12xy+8y^2\) преобразуется к каноническому виду \(\Phi(x, y)=5(x')^2+20(y')^2,\) а заданное уравнение — к виду$$5(x')^2+20(y')^2-20=0,$$или$$\frac{(x')^2}4+\frac{(y')^2}1=1.$$ Данная линия — эллипс.
Можно указать и базис, в котором уравнение эллипса принимает канонический вид. Его легко получить исходя из собственных векторов линейного преобразования с матрицей \(A.\) Для этого найдём собственные векторы линейного преобразования.
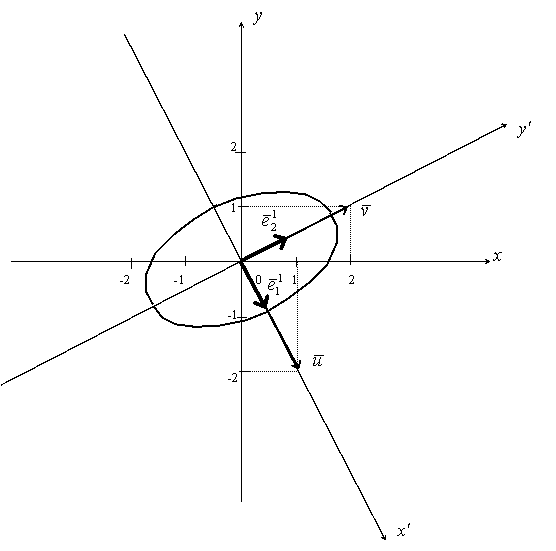
Для \(\lambda_1=5\) получим систему$$\begin{cases}(17-5)x+6y=0,\\6x+(8-5)y=0,\end{cases}$$или$$\begin{cases}12x+6y=0,\\6x+3y=0.\end{cases}$$ Отсюда \(y=-2x\) и мы имеем собственный вектор$$\vec u=\begin{pmatrix}1\\-2\end{pmatrix}.$$ Для \(\lambda_2=20\) получим систему$$\begin{cases}(17-20)x+6y=0,\\6x+(8-20)y=0,\end{cases}$$или$$\begin{cases}-3x+6y=0,\\6x-12y=0.\end{cases}$$ Отсюда \(y=0,5x\) и мы имеем собственный вектор$$\vec v=\begin{pmatrix}2\\1\end{pmatrix}.$$ Предполагая, что исходный базис есть ортонормированный базис, находим длину вектора \(\vec u,\) равную$$|\vec u|=\sqrt{1^2+(-2)^2}=\sqrt5.$$ Тогда единичный вектор, сонаправленный с \(\vec u,\) будет$$\vec e'_1=\begin{vmatrix}\frac1{\sqrt5}\\-\frac2{\sqrt5}\end{vmatrix}.$$ Аналогично, длина вектора \(\vec v\) равна$$|\vec v|=\sqrt{2^2+1^2}=\sqrt5$$и единичный вектор, сонаправленный с \(\vec v,\) будет$$\vec e'_2=\begin{vmatrix}\frac2{\sqrt5}\\\frac1{\sqrt5}\end{vmatrix}.$$ Базис \(\{\vec e'_1, \, \vec e'_2\}\) является искомым базисом, в котором данное уравнение принимает канонический вид. Если обозначить векторы исходного базиса через \(\vec e_1, \, \vec e_2,\) то$$\vec e'_1=\frac1{\sqrt5}\vec e_1-\frac2{\sqrt5}\vec e_2, \quad \vec e'_2=\frac2{\sqrt5}\vec e_1+\frac1{\sqrt5}\vec e_2.$$ Формулы преобразования координат$$\begin{cases}x=\frac1{\sqrt5}x'+\frac2{\sqrt5}y',\\y=-\frac2{\sqrt5}x'+\frac1{\sqrt5}y'.\end{cases}$$ Сделаем чертёж.