Задача 11. Найти область сходимости функционального ряда.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
11.6. Найти область сходимости функционального ряда
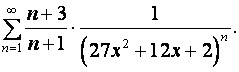
Решение.
Общий член ряда
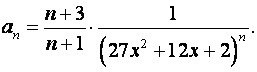
Согласно радикальному признаку Коши, ряд сходится абсолютно, если
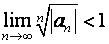
то есть, область сходимости функционального ряда удовлетворяет неравенству
Отсюда для области сходимости ряда получим
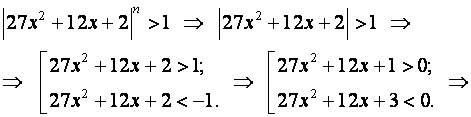
Решим первое неравенство.
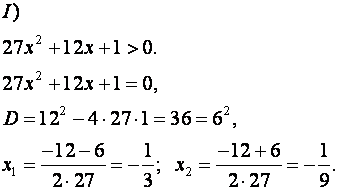
Следовательно,
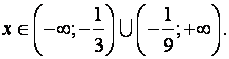
Решим второе неравенство.
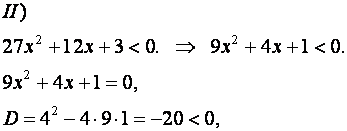
Следовательно, корней нет. Неравенство не имеет решений. Таким образом, интервал сходимости
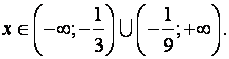
Исследуем сходимость ряда на концах интервала. Пр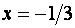и 
и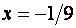 
исходный ряд запишется
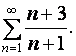
Этот ряд расходится по необходимому условию. Таким образом, область сходимости ряда
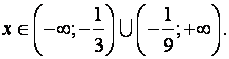
Ответ: Область сходимости функционального ряда
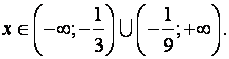
11.15 Найти область сходимости функционального ряда
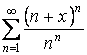
Решение.
Общий член ряда
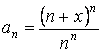
Тогда для любого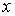 
из области сходимости ряда предел
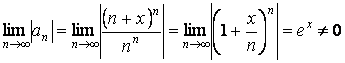
Следовательно, по необходимому условию сходимости, функциональный ряд расходится при всех .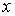
Область сходимости функционального ряда представляет собой пустое множество.
11.16 Найти область сходимости функционального ряда
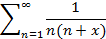
Решение.
Рассмотрим неотрицательные х. В этом случае функциональный ряд всегда сходится.
Действительно:
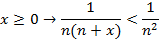
а числовой ряд
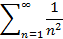
сходится, как ряд Дирихле.
Рассмотрим отрицательные х. Тогда, если х есть НЕ целое число, то
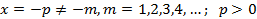
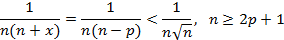
и по предельному признаку сравнения функциональный ряд также сходится как и ряд
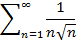
Рассмотрим теперь случай отрицательных целых х. Тогда в сумме всегда найдется слагаемое с равным нулю знаменателем. В этом случае ряд расходится.
Таким образом, область сходимости ряда — все действительные х, за исключением целых отрицательных значений