Электромагнетизм

Контрольная работа 4.
ЭЛЕКТРОМАГНЕТИЗМ

Введите номер задачи и нажмите кнопку "Решение", или решите задачу на основании нижепредставленных формул.

Основные формулы по курсу "Электромагнетизм" и "Магнитное поле"

Связь магнитной индукции $\mathbf B$ с напряжённостью магнитного поля $\mathbf H$ $$ \mathbf B = \mu \mu_0 \mathbf H, $$где $\mu$ — магнитная проницаемость изотропной среды; $\mu_0$ — магнитная постоянная $\left(\mu_0=4\pi\cdot 10^{-7}Гн/м\right)$. В вакууме $\mu=1$, и тогда магнитная индукция в вакууме $$ \mathbf B = \mu_0 \mathbf H. $$ Закон Био — Савара — Лапласа $$ d\mathbf B={{\mu\mu_0}\over{4\pi}}[d\mathbf l, \mathbf r]{l\over{r^2}} \qquad или \qquad dB={{\mu\mu_0}\over{4\pi}}{{lsin\alpha}\over{r^2}}dl,$$где $d\mathbf B$ — магнитная индукция поля, создаваемого элементом провода $dl$ c током $I$; $\mathbf r $ — радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; $\alpha$ — угол между радиусом-вектором и направлением тока в элементе провода.

Магнитная индукция в центре кругового тока$$ B={{\mu\mu_0 I}\over{2R}},$$где $R$ — радиус кругового витка.

Магнитная индукция на оси кругового тока $$ B={{\mu\mu_0}\over{4\pi}}\cdot {{2\pi R^2 I}\over{\left(R^2+h^2\right)^{3/2}}},$$где $h$ — расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока$$ B={{\mu\mu_0 I}\over{2\pi r_0}},$$где $r_0$ — расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода я с током (см. рис), $$ B={{\mu\mu_0 I}\over{4\pi r_0}}\left(cos \alpha_1-cos \alpha_2\right).$$ Обозначения ясны из рисунка. Направление вектора магнитной индукции $\mathbf B$ обозначено точкой — это значит, что вектор $\mathbf B$ направлен перпендикулярно плоскости чертежа к нам.

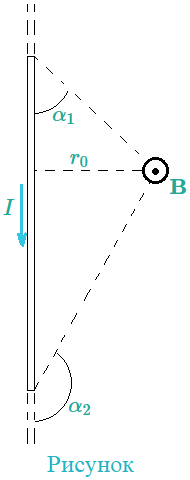
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция, $\alpha_2=\pi-\alpha_1 \quad и \quad -cos\alpha_2=cos\alpha_1=cos\alpha$, тогда $$B={{\mu\mu_0}\over{2\pi}}{I\over{r_0}} cos \alpha.$$

Магнитная индукция поля соленоида $$B=\mu\mu_0 nI,$$где $n$ — отношение числа витков соленоида к его длине.

Сила, действующая на провод с током в магнитном поле (закон Ампера),$$\mathbf F =I[\mathbf l, \mathbf B], \qquad или \qquad F=IBlsin\alpha, $$где $l$ — длина провода; $\alpha$ — угол между направлением тока в проводе и вектором магнитной индукции $\mathbf B$. Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применить к каждому элементу провода в отдельности:$$d \mathbf F =I[d \mathbf l, \mathbf B].$$ Магнитный момент плоского контура с током$$ \mathbf p_m= \mathbf n IS,$$где $\mathbf n$ — единичный вектор нормали (положительной) к плоскости контура; $I$ — сила тока, протекающего по контуру; $S$ — площадь контура.

Механический момент (вращательный) , действующий на контур с током, помещённый в однородное магнитное поле,$$ \mathbf M= [\mathbf p_m, \mathbf B], \qquad или \qquad M=p_mBsin\alpha,$$где $\alpha$ — угол между векторами $ \mathbf p_m$ и $\mathbf B$.

Потенциальная энергия (механическая) контура с током в магнитном поле$$\Pi_{мех}=-\left(\mathbf p_m, \mathbf B\right), \qquad или \qquad \Pi_{мех}=- p_m B cos \alpha.$$ Отношение магнитного момента $p_m$ к механическому $L$ (моменту импульса) заряженной частицы, движущейся по круглой орбите, $${{p_m}\over L}=\frac12 \frac Qm,$$где $Q$ — заряд частицы; $m$ —масса частицы.

Сила Лоренца $$\mathbf F=Q[\mathbf v, \mathbf B], \qquad или \qquad F=QvBsin\alpha,$$где $\mathbf v$ — скорость заряженной частицы; $\alpha$ — угол между векторами $\mathbf v$ и $\mathbf B$.

Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение $$\mathbf F=Q \mathbf E + Q[\mathbf v, \mathbf B].$$ Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности $$\Phi=BScos\alpha, \qquad или \qquad \Phi=B_n S,$$где $S$ — площадь контура; $\alpha$ — угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности $$\Phi=\int_S B_ndS$$ (интегрирование ведётся по всей поверхности).

Потокосцепление (полный поток) $$\Psi=N\Phi.$$Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу $N$ витков.

Работа по перемещению замкнутого контура в магнитном поле $$A=I\Delta\Phi.$$ ЭДС индукции $$\mathscr E=-{{d\Psi}\over{dt}}.$$ Разность потенциалов на концах провода, движущегося со скоростью $\mathbf v$ в магнитном поле, $$U=Blvsin\alpha,$$где $l$ — длина провода; $\alpha$ — угол между векторами $\mathbf v$ и $\mathbf B$.

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур, $$Q={{\Delta\Phi}\over R}, \qquad или \qquad Q={{N \Delta\Phi}\over R}={{\Delta\Psi}\over R},$$где $R$ — сопротивление контура.

Индуктивность контура $$L=\frac \Phi I.$$ ЭДС самоиндукции $$L=\mathscr E_s=-L {{dI}\over{dt}}.$$ Индуктивность соленоида $$L=\mu \mu_0 n^2 V,$$где $n$ — отношение числа витков соленоида к его длине; $V$ — объём соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением $R$ и индуктивностью $L$:

а) $ \quad I={{\mathscr E}\over R} \left(1-e^{-Rt/L}\right) \quad$ (при замыкании цепи), где $\mathscr E $ — ЭДС источника тока; $t$ — время, прошедшее после замыкания цепи;

б) $ \quad I=I_0 e^{-Rt/L} \quad$ (при размыкании цепи), где $I_0 $ — сила тока в цепи при $t=0; \; t$ — время, прошедшее c момента размыкания цепи.

Энергия магнитного поля $$W={{LI^2}\over 2}.$$ Объёмная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объёму)$$w={{BH}\over 2}, \qquad или w={{B^2}\over {2\mu \mu_0}}, \qquad или \qquad w={{\mu \mu_0 H^2}\over 2},$$где $B$ — магнитная индукция; $B$ — напряжённость магнитного поля.

К. Р. 3 В начало К. Р. 5