
Проекция средней скорости на ось \(x\) $$ \left< v_x \right>= {\Delta x \over \Delta t}. $$
Средняя путевая скорость \(x\) $$ \left< v \right>= {\Delta s \over \Delta t}, $$
где \(\Delta s\) — путь, пройденный точкой за интервал времени \(\Delta t\).
Проекция мгновенной скорости на ось \(x\) $$ v_x = {d x \over d t}. $$
Проекция среднего ускорения на ось \(x\) $$ \left< a_x \right>= {\Delta v_x \over \Delta t}. $$
Проекция мгновенного ускорения на ось \(x\) $$ a_x = {d v_x \over d t}. $$
Модуль угловой скорости $$ \omega = {d\varphi \over d t}. $$
Модуль углового ускорения $$ \varepsilon = {d\omega \over d t}. $$
Формулы по физике, устанавливающие связь между модулями линейных и угловых величин:$$ v=\omega\cdot R, \qquad \qquad a_\tau = \varepsilon \cdot R, \qquad \qquad a_n= \omega^2 \cdot R, $$ где \(v\) — модуль линейной скорости; \(a_\tau\) и \(a_n\) — модули тангенциального и нормального ускорений; \(\omega\) — модуль угловой скорости; \(\varepsilon\) — модуль углового ускорения; \(R\) — радиус окружности.
Модуль полного ускорения$$ a=\sqrt{a_\tau^2+a_n^2}, \qquad или \qquad a=R\sqrt{\varepsilon^2+\omega^4}.$$
Угол между полным \(a\) и нормальным \(a_n\) ускорениями $$ \alpha =arccos(a_n / a). $$
Кинематическое уравнения гармонических колебаний материальной точки$$ x=Acos(\omega t+\varphi), $$ где \(x\) — смещение; \(A\) — амплитуда колебаний; \(\omega\) — угловая или циклическая частота; \(\varphi\) — начальная фаза.
Скорость и ускорение материальной точки, совершающей гармонические колебания:$$ v=-A\omega sin(\omega t+\varphi); \qquad \qquad a=-A\omega^2 cos(\omega t+\varphi). $$
Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания $$ A=\sqrt{A_1^2+A_2^2+2A_1A_2cos(\varphi_2-\varphi_1)}; $$ б) начальная фаза результирующего колебания$$ \varphi=arctg{{A_1sin\varphi_1+A_2sin\varphi_2} \over {A_1cos\varphi_1+A_2cos\varphi_2}}. $$
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,
$$ x=A_1cos\omega t; \qquad \qquad y=A_2cos(\omega t+\varphi). $$ a) \( x={A_2 \over A_1}x, \) если разность фаз \(\varphi=0;\)
б) \( x=-{A_2 \over A_1}x, \) если разность фаз \(\varphi=\pi\) или \(\varphi=-\pi; \)
в) \({x^2 \over A_1^2}+{y^2 \over A_2^2}=1\), если разность фаз \(\varphi={\pi \over 2}\) или \(\varphi=-{\pi \over 2}\).
Уравнение плоской бегущей волны $$ y=Acos\omega \left( t-\frac x v\right),$$ где \(y\) — смещение любой из точек среды с координатой \(x\) в момент времени \(t\); \(v\) — скорость распространения колебаний в среде.
Связь разности фаз \(\Delta\varphi\) колебаний с расстоянием \(\Delta x\) между точками среды, отсчитанным в направлении распространения колебаний; $$ \Delta\varphi = {{2\pi}\over\lambda}\Delta x, $$ где \(\lambda\) — длина волны.
Импульс материальной точки массой \(m\), движущейся со скоростью \(\vec v\), $$ \vec p=m\vec v. $$
Второй закон Ньютона $$ d\vec p=\vec F dt, \qquad или \qquad \vec F =m \vec a, $$ где \(\vec F\) — результирующая сила, действующая на материальную точку; \(\vec a\) — полное ускорение точки.
Силы, рассматриваемые в механике:
а) сила упругости$$ F=-kx,$$где \(k\) — коэффициент упругости (в случае пружины — жёсткость); \(x\) — абсолютная деформация;
б) сила тяжести $$ P=mg,$$где \(g=9,81 {м \over с^2}\) — ускорение свободного падения (напряжённость гравитационного поля);
в) сила гравитационного взаимодействия$$ F=G{{m_1m_2}\over r^2},$$где \(G=6,67\cdot 10^{-11}{кг\over{м\cdot c^2}}\) — гравитационная постоянная; \(m_1\) и \(m_2\) — массы взаимодействующих тел; \(r\) — расстояние между телами (тела рассматриваются как материальные точки) или между центрами тел, если тела имееют шарообразнную форму, как, например, планеты и звёзды. В случае гравитационного взаимодействия силу можно выразить также через напряжённость \(\vec g\) гравитационного поля:$$ \vec F=m \vec g;$$
г) сила трения (скольжения) $$ F=\mu N,$$ где \(\mu \) — коэффициент трения; \(N\) — сила нормального давления (реакция опоры). Сила трения покоя определяется как сила, противоположная равнодействующей остальных сил, действующих на тело.
Закон сохранения импульса$$ \sum_{i=1}^n{p_i}=const, $$ или для двух тел \(n=2\)$$m_1v_1+m_2v_2=m_1u_1+m_2u_2,$$ где \(v_1\) и \(v_2\) — скорости тел в момент времени, принятый за начальный; \(u_1\) и \(u_2\) — скорости тех же тел в момент времени, принятый за конечный.
Физическая формула, выражающая кинетическую энергию тела:$$ T={mv^2 \over 2} \qquad или \qquad T={p^2 \over 2m.}$$ Потенциальная энергия:
а) упругодеформированной пружины$$ \Pi={kx^2 \over 2},$$где \(k\) — жёсткость пружины; \(x\) — абсолютная деформация;
б) гравитационного взаимодействия $$ \Pi=-G{{m_1m_2} \over r},$$где \(G\) — гравитационная постоянная; \(m_1\) и \(m_2\) — массы взаимодействующих тел; \(r\) — расстояние между ними (тела рассматриваются как материальные точки) или между центрами тел, если тела имееют шарообразнную форму (звёзды, планеты).
в) тела, находящегося в однородном поле силы тяжести, $$\Pi=mgh, $$где \(m\) — масса тела; \(g\) — ускорение свободного падения; \(h\) —высота тела над уровнем, принятым за нулевой (формула справедлива при условии \(h \lt \lt R \), где \(R=6378 км\) — радиус Земли).
Закон сохранения механической энергии $$E=T+\Pi=const.$$ Работа \(A\) как изменение кинетической энергии: $$A=\Delta T=T_2-T_1.$$ Работа силы \(\vec F\) на перемещении \(\vec s\) равна скалярному произведению векторов \(\vec F\) и \(\vec s\)$$ A=\left(\vec F,\vec s\right)=F\cdot s \cdot cos\alpha,$$где \(\alpha\) — угол между векторами \(\vec F\) и \(\vec s\).
Мгновенная мощность есть производная работы по времени $$P={dA \over dt}.$$
Средняя мощность или работа, совершаемая в единицу времени, равна $$ \left< P \right> ={A \over t}.$$
Коэффициент полезного действия (КПД): $$ \eta = {A_п \over A_з}\cdot 100 ^o/_o , $$где \(A_п\) — полезная работа, \(A_з\) — затраченная работа.
Основное уравнение динамики вращательного движения относительно неподвижной оси \(z\) $$M_z=J_z\varepsilon,$$ где \(M_z\) — результирующий момент внешних сил относительно оси \(z\), действующих на тело; \(\varepsilon\) — угловое ускорение; \(J_z\) — момент инерции относительно оси вращения.
Моменты инерции некоторых тел массой \(m\) относительно оси \(z\), проходящей через центр масс:
а) стержня длиной \(l\) относительно оси, перпендикулярной стержню,$$J_z={1 \over {12}}ml^2;$$ б) обруча (тонкостенного цилиндра) радиуса \(R\) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра), $$J_z=mR^2;$$ в) диска (сплошного цилиндра) радиуса \(R\) относительно оси, перпендикулярной плоскости диска (совпадающей с осью цилиндра), $$J_z={1 \over 2}mR^2;$$ г) шара радиуса \(R\) относительно любой оси, проходящей через его центр $$J_z={2 \over 5}mR^2.$$
Момент инерции \(J\) относительно оси, не проходящей через центр масс, определяется теоремой Штейнера $$ J=J_0+ma^2,$$ где \(J_0\) — момент инерции относительно параллельной центральной оси; \(a\) — расстояние между осями.
Проекция на ось \(z\) момента импульса тела, вращающегося относительно неподвижной оси \(z\) с угловой скоростью \(\omega\), $$ L_z=J_z\omega.$$
Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси \(z\),$$J_z\omega=const, $$где \(J_z\) — момент инерции системы тел относительно оси \(z\); \(\omega\) — угловая скорость вращения системы тел относсительно оси \(z\).
Формула по физике для кинетической энергии вращающегося тела \(z\),$$T=\frac12 J_z\omega^2 \qquad или \qquad T={{L_z^2}\over {2J_z}}. $$
Молекулярная физика и Термодинамика
Количество вещества $$ \nu = {N\over{N_A}}, $$где \(N\) — число структурных элементов (молекул, атомов, ионов), составляющих тело; \(N_A\) — постоянная Авогадро ( \(N_A=6,02\cdot10^{23} моль^{-1}\)).
Молярная масс вещества $$ \mu= {m \over \nu}, $$ где \(m\) — масса вещества; \(\nu\) — количество вещества.
Относительная молекулярная масса вещества $$ M_r=\sum n_iA_{r,i},$$где \(n_i\) — число атомов \(i\) - го химического элемента, входящих в состав молекулы данного вещества; \(A_{r,i}\) — относительная атомная масса этого вещества.
Связь молярной массы \(\mu\) с относительной молекулярной массой вещества \(M_r\) определяется формулой $$ \mu = {{M_r} \over {1000}}. $$ Количество вещества смеси газов $$ \nu=\nu_1+\nu_2+...+\nu_n={{N_1}\over{N_A}}+{{N_2}\over{N_A}}+...+{{N_n}\over{N_A}}, $$или $$ \nu=={{m_1}\over{\mu_1}}+{{m_2}\over{\mu_2}}+...+{{m_n}\over{\mu_n}}, $$ где \(\nu_i, N_i, m_i, \mu_i\) — соответственно количество вещества, число молекул, масса, молярная масса \(i\)-го компонента смеси.
Термодинамическая или абсолютная температура $$T=t^oC+273,$$где \(t^oC\) — температура по шкале Цельсия.
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа) $$ pV={m \over \mu}RT=\nu RT, $$ где \(m\) — масса газа, \(\mu\) — молярная масса газа, \(\nu\) — количество вещества, \(T\) — термодинамическая температура газа, \(R\) — универсальная газовая постоянная
\(\left(R=8,31{{Дж}\over{К\cdot моль}}\right)\).
Газовые законы для изопроцессов:
а) закон Бойля – Мариотта (изотермический процесс: \(T=const, m=const\)) $$ pV = const, $$ или для двух состояний газа $$ p_1V_1 = p_2V_2; $$
б) закон Гей – Люссака (изобарный процесс: \(p=const, m=const\)) $$ \frac V T = const, $$ или для двух состояний $$ {{V_1}\over{T_1}} = {{V_2}\over{T_2}}; $$ в) закон Шарля (изохорный процесс: \(V=const, m=const\)) $$ \frac p T = const, $$ или для двух состояний $$ {{p_1}\over{T_1}} = {{p_2}\over{T_2}}; $$ г) объединённый или универсальный газовый закон (\(m=const\)) $$ {{pV}\over T} = const, \qquad или \qquad {{p_1V_1}\over{T_1}} = {{p_2V_2}\over{T_2}}, $$ где \(p_1, V_1, T_1\) — давление, объём и температура газа в начальном состоянии;
\(p_2, V_2, T_2\) — давление, объём и температура газа в конечном состоянии.
Закон Дальтона, определяющий давление смеси газов, $$ p=p_1+p_2+...+p_n, $$ где \(p_i\) — парциальные давления компонентов смеси; \(n\) — число компонентов смеси.
Молярная масса смеси газов $$ \mu ={{m_1+m_2+...+m_n}\over{\nu_1+\nu_2+...+\nu_n}}, $$ где \(m_i\) — масса \(i\)-го компонента смеси; \(\nu_i={{m_i}\over{\mu_i}}\) — количество вещества \(i\)-го компонента смеси; \(n\) — число компонентов смеси.
Массовая доля \(i\)-го компонента смеси газа $$ w_i={{m_i}\over m}, $$ где \(m\) — масса смеси.
Концентрация молекул $$ n=\frac N V = {{N_A \rho}\over \mu}. $$ где \(N\)
— число молекул газа (тела); \(\rho, V\) — плотность и объём газа (тела).
Основное уравнение молекулярно-кинетической теории газов $$ p=\frac23 n \left<\varepsilon_п\right>, $$ где \(\left<\varepsilon_п\right>\) — средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия поступательного движения молекулы $$ \left<\varepsilon_п\right> = \frac32 kT,$$ где \(k\) — постоянная Больцмана \(\left(k=1,38\cdot10^{-23}{{Дж}\over К}\right)\).
Средняя полная кинетическая энергия молекулы $$ \left<\varepsilon_i\right> = \frac i2 kT,$$ где \(i\) — число степеней свободы молекулы.
Зависимость давления газа от концентрации молекул и температуры $$p=nkT.$$ Формулы по физике для скорости молекул:
$$ \left< v_{кв} \right> = \sqrt{{{3kT} \over {m_0}}}= \sqrt{{{3RT} \over {\mu}}} \, — \, средняя \, квадратичная; $$ $$ \left< v \right> = \sqrt{{{8kT} \over {\pi m_0}}} = \sqrt{{{8RT} \over {\pi \mu}}} \, — \, средняя \, арифметическая; $$ $$ v_в = \sqrt{{{2kT} \over {m_0}}} = \sqrt{{{2RT} \over {\mu}}} \, — \, наиболее \, вероятная, $$ где \(m_0\) — масса одной молекулы.
Относительная скорость молекулы $$ u={v \over {v_в}}, $$ где \(v\) — скорость молекулы.
Удельная теплоёмкость газа при постоянном объёме \( \left( c_V \right) \) и постоянном давлении \( \left( c_p \right) \) $$ c_V = \frac i2 \frac R\mu, \qquad \qquad c_p = {{i+2} \over 2} \frac R\mu. $$ Связь между удельной \(c\) и молярной \(C\) теплоёмкостями $$ c = \frac C \mu, \qquad \qquad C = c \mu. $$ Уравнение Майера $$С_p-C_V=R.$$ Внутренняя энергия
идеального газа $$U= \frac m\mu \frac i2 RT = \frac m\mu C_VT.$$ Первый закон термодинамики $$Q=A+\Delta U,$$где \(Q\) — теплота, сообщённая газу (телу); \(\Delta U\) — изменение внутренней энергии газа (тела); \(A\) — работа, совершённая газом против внешних сил.
Формула по физике для работа газа:$$ A=\int_{V_1}^{V_2}p \Delta V \quad в \, общем \, случае; $$ $$ A=p\left(V_2-V_1\right) \quad при \, изобарном \, процессе; $$ $$ A= \frac m \mu RT ln{{V_2} \over {V_1}} \quad при \, изотермическом \, процессе;$$ $$ A= - \Delta U = - \frac m \mu C_V \Delta T, \qquad или \qquad A={{RT_1} \over {\gamma -1}} \frac m \mu \left[1-\left({{V_1} \over {V_2}}\right)^{\gamma -1} \right]$$ при адиабатном процессе, где \(\gamma={{c_p} \over {c_V}}\) — показатель адиабаты.
Уравнение Пуассона, связывающие параметры идеального газа при адиабатном процессе:
$$pV^\gamma=const, \qquad {{T_2} \over {T_1}} = \left({{V_1} \over {V_2}}\right)^{\gamma -1},$$ $${{p_2} \over {p_1}} = \left({{V_1} \over {V_2}} \right)^\gamma, \qquad {{T_2} \over {T_1}} = \left({{p_2} \over {p_1}}\right)^{{\gamma -1} \over \gamma}.$$
КПД цикла $$\eta={{Q_1-Q_2} \over {Q_1}},$$ где \(Q_1\) — теплота, полученная рабочим телом (газом) от теплоотдатчика; \(Q_2\) — теплота, переданная рабочим телом (газом) теплоприёмнику.
Термический КПД цикла Карно $$\eta={{Q_1-Q_2} \over {Q_1}}={{T_1-T_2} \over {T_1}},$$ где \(T_1\) и \(T_2\) — термодинамические температуры теплоотдатчика и теплоприёмника.
Коэффициент поверхностного натяжения $$ \alpha = \frac Fl, \qquad или \qquad \alpha = {{\Delta E} \over {\Delta S}}, $$ где \(F\) — сила поверхностного натяжения, действующая на контур \(l\), ограничивающий поверхность жидкости; \(\Delta E\) — изменение
свободной энергии поверхностной плёнки жидкостм, связанное с изменением площади \(\Delta S\) поверхности этой плёнки.
Формула Лапласа, выражающая давление \(p\), создаваемое сферической поверхностью жидкости: $$p={{2\alpha}\over R},$$где \(R\) — радиус сферической поверхности.
Высота подъёма жидкости в капиллярной трубке $$h={{2\alpha cos\theta}\over{\rho g R}},$$где \(\theta\) — краевой угол (\(\theta=0\) при полном смачивании стенок трубки жидкостью; \(\theta=\pi\) при полном несмачивании); \(R\) — радиус канала трубки; \(\rho\) — плотность жидкости; \(g\) — ускорение свободного падения.
Высота подъёма жидкости между двумя близкими и параллельными плоскостями$$h={{2\alpha cos\theta}\over{\rho g d}},$$где \(d\) — расстояние между плоскостями.
Электростатика и постоянный электрический ток
Закон Кулона $$ F={{Q_1Q_2} \over {4\pi \varepsilon_0 \varepsilon r^2}}, $$ где \(F\) — сила взаимодействия точечных зарядов \(Q_1\) и \(Q_2\); \(r\) — расстояние между зарядами; \(\varepsilon\) — диэлектрическая проницаемость; \(\varepsilon_0\) — электрическая постоянная \( \left( \varepsilon_0 = 8,85\cdot 10^{-12} \frac Ф м \right) \).
Формулы по физике для напряжённости и потенциала электрического поля: $$ \vec E = {\vec F \over Q}, \qquad \qquad \varphi = {\Pi \over Q}, $$ где \(\Pi\) — потенциальная энергия точечного положительного заряда \(Q\), находящегося в данной точке поля.
Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда $$ \vec F = Q \vec E, \qquad \qquad \Pi=Q \varphi.$$
Напряжённость и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей), $$ \vec E=\sum_{i=1}^N \vec E_i, \qquad \qquad \varphi=\sum_{i=1}^N \varphi_i,$$где \(\vec E_i, \varphi_i\) — напряжённость и потенциал в данной точке поля, создаваемого \(i\)-м зарядом.
Напряжённость и потенциал поля, создаваемого точечным зарядом, $$ E={Q \over {4\pi \varepsilon_0 \varepsilon r^2}}, \qquad \qquad \varphi={Q \over {4\pi \varepsilon_0 \varepsilon r}},$$ где \(r\) — расстояние от заряда \(Q\) до точки, в которой определяются напряжённость и потенциал.
Напряжённость и потенциал поля, создаваемого проводящей заряженной сферой радиусом \(R\) на расстоянии \(r\) от центра сферы:
а) \( E=0; \qquad \varphi = { Q \over {4 \pi \varepsilon_0 \varepsilon R}}\) (при \(r < R\) ) ;
б) \(E= {Q \over {4\pi \varepsilon_0 \varepsilon R^2}}; \qquad \varphi = {Q \over {4\pi \varepsilon_0 \varepsilon R}} \qquad \) (при \(r=R\));
в) \(E= {Q \over {4\pi \varepsilon_0 \varepsilon r^2}}; \qquad \varphi = {Q \over {4\pi \varepsilon_0 \varepsilon r}} \qquad \) (при \(r>R\)),
где \(Q\) — заряд сферы.
Линейная плотность заряда \( \qquad \qquad \tau = Q/l. \)
Поверхностная плотность заряда \( \qquad \qquad \sigma = Q/S.\)
Напряжённость и потенциал поля, создаваемого распределёнными зарядами: $$ E = {{\tau} \over {4\pi \varepsilon_0 \varepsilon}} \cdot \int_l {{dl} \over r^2}\cdot {{\vec r}\over r}; \qquad \qquad \varphi = {{\tau } \over {4\pi \varepsilon_0 \varepsilon}}\int_l {{dl} \over r^2}.$$
Напряжённость поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром, $$E={{\tau} \over {2\pi \varepsilon_0 \varepsilon r}}.$$где \(r\) — расстояние от нити или оси цилиндра до точки, напряжённость поля в которой определяется.
Напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью, $$E={\sigma \over {2\varepsilon_0 \varepsilon}},$$где \(\sigma\) — поверхностная плотность заряда, распределённого по плоскости.
Связь потенциала с напряжённостью:
а) \(\vec E=-grad \varphi, \qquad или \qquad \vec E =-\left(\vec i {{\partial \varphi}\over{\partial x}}+\vec j {{\partial \varphi}\over{\partial y}}+\vec k {{\partial \varphi}\over{\partial z}}\right) \qquad \) в общем случае;
б) \(E=\left(\varphi_1-\varphi_2\right)/d\) в случае однородного поля;
в) \(E=-{{d\varphi}\over{dr}}\) в случае поля, обладающего центральной или осевой симметрией.
Электрический момент диполя \(\qquad \vec p =|Q|\vec l, \qquad \), где \(Q\) — заряд; \(\vec l\) — плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Формула для работы сил электростатического поля по перемещению заряда \(Q\) из точки поля с потенциалом \(\varphi_1\) в точку с потенциалом \(\varphi_2\) $$A_{12}=Q \left( \varphi_1-\varphi_2 \right) .$$
Электроёмкость $$С=\frac Q \varphi, \qquad или \qquad С=\frac QU,$$где \(\varphi\) — потенциал проводника; \(U\) — разность потенциалов пластин конденсатора.
Электроёмкость плоского конденсатора$$С={{\varepsilon_0 \varepsilon S}\over d}$$где \(S\) — площадь пластины (одной) конденсатора; \(d\) — расстояние между пластинами.
Электроёмкость батареи конденсаторов:$$ \qquad а) \quad \frac1C=\sum_{i=1}^N {1 \over {C_i}} \qquad при \, последовательном \, соединении;$$ $$ б) \quad C=\sum_{i=1}^N C_i \qquad при \, параллельном \, соединении,$$где \(N\) — число конденсаторов в батарее.
Энергия заряженного конденсатора:$$W={{QU}\over 2}, \qquad \qquad W={{CU^2}\over 2}, \qquad \qquad W={{Q^2}\over {2C}}. $$
Сила постоянного тока \( \quad I=Q/l, \quad \) где \(Q\) — заряд, прошедший через поперечное сечение проводника за время \( t\).
Плотность тока \( \quad j=I/S, \quad \) где \(Q\) — площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью \( < v > \) направленного движения заряженных частиц $$ j=Qn < v > ,$$где \(Q\) — заряд частицы; \(n\) — концентрация заряженных частиц.
Закон Ома:
а) \( \quad I={{\varphi_1-\varphi_2} \over R} = \frac UR \quad \) для участка цепи, не содержащего ЭДС, где \(\varphi_1-\varphi_2=U \) — разность потенциалов (напряжение) на концах участка; \(R\) — сопротивление участка;
б) \( \quad I={{\left( \varphi_1-\varphi_2 \right) + \mathscr E }\over R} \quad \) для участка цепи, содержащего ЭДС, где \(\mathscr E \) — ЭДС источника тока; \(R\) — полное сопротивление участка (сумма внешних и внутренних сопротсвлений);
в) \( \quad I={{\mathscr E }\over {R+R_i}} \quad \) для замкнутой (полной) цепи, содержащей ЭДС, где \(R \) — внешнее сопротивление цепи; \(R_i\) — внутреннее сопротивление цепи.
Законы Киргофа:
а) \( \quad \sum I_i\) — первый закон;
б) \( \quad \sum I_iR_i=\sum \mathscr E_i\) — второй закон,
где \(\sum I_i \) — алгебраическая сумма сил токов, сходящихся в узле; \(\sum I_iR_i\) — алгебраическая сумма произведений сил токов на сопротивления участков; \( \sum \mathscr E_i\) — алгебраическая сумма ЭДС.
Сопротивление \(R\) и проводимость \(G\) проводника $$ R={{\rho l}\over S}, \qquad G={{\gamma S}\over l}, $$где \(\rho\) — удельное сопротивление; \(\gamma\) — удельная проводимость; \(l\) — длина проводника; \(S\) — площадь поперечного сечения проводника.
Сопротивление системы проводников:
а) \(\quad R=\sum R_i \quad\) при последовательном соединении; б) \(\quad \frac1R=\sum \frac1R_i \quad\) при параллельном соединении, где \(R_i\) — сопротивление \(i\)-го проводника.
В случае двух проводников: при последовательном соединении общее сопротивление равно \(R=R_1+R_2\); при параллельном соединении общее сопротвление равно$$R={{R_1R_2}\over{R_1+R_2}}.$$
Работа тока: $$ A=UIt, \qquad A=I^2Rt, \qquad A={{U^2t}\over R}. $$ Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение \(U\), последние две — для участка, не содержащего ЭДС.
Закон Джоуля – Ленца: В проводнике сопротивлением \(R\), по которому течёт ток \(I\), за время \(t\) выделяется тепло $$ Q=I^2Rt.$$
Закон Ома в дифференциальной форме $$ \vec j =\gamma \vec E, $$где \(\gamma\) — удельная проводимость; \(E\) — напряжённость электрического поля; \(\vec j\) — плотность тока.
Связь удельной проводимости \( \gamma \) с подвижностью \(b\) — заряженных частиц (ионов) $$\gamma=Qn\left(b_++b_-\right),$$где \(Q\) — заряд ионов; \(n\) — концентрация ионов; \(b_+\) и \(b_-\) — подвижности положительных и отрицательных ионов.
Электромагнетизм и магнитное поле
Физическое уравнение, устанавливающее связь магнитной индукции \(\mathbf B\) с напряжённостью магнитного поля \(\mathbf H\) $$ \mathbf B = \mu \mu_0 \mathbf H, $$где \(\mu\) — магнитная проницаемость изотропной среды; \(\mu_0\) — магнитная постоянная \(\left(\mu_0=4\pi\cdot 10^{-7}Гн/м\right)\). В вакууме \(\mu=1\), и тогда магнитная индукция в вакууме $$ \mathbf B = \mu_0 \mathbf H. $$
Закон Био — Савара — Лапласа $$ d\mathbf B={{\mu\mu_0}\over{4\pi}}[d\mathbf l, \mathbf r]{l\over{r^2}} \qquad или \qquad dB={{\mu\mu_0}\over{4\pi}}{{lsin\alpha}\over{r^2}}dl,$$где \(d\mathbf B\) — магнитная индукция поля, создаваемого элементом провода \(dl\) c током \(I\); \(\mathbf r \) — радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; \(\alpha\) — угол между радиусом-вектором и направлением тока в элементе провода.
Магнитная индукция в центре кругового тока$$ B={{\mu\mu_0 I}\over{2R}},$$где \(R\) — радиус кругового витка.
Магнитная индукция на оси кругового тока $$ B={{\mu\mu_0}\over{4\pi}}\cdot {{2\pi R^2 I}\over{\left(R^2+h^2\right)^{3/2}}},$$где \(h\) — расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока$$ B={{\mu\mu_0 I}\over{2\pi r_0}},$$где \(r_0\) — расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода я с током (см. рис), $$ B={{\mu\mu_0 I}\over{4\pi r_0}}\left(cos \alpha_1-cos \alpha_2\right).$$
Обозначения ясны из рисунка. Направление вектора магнитной индукции \(\mathbf B\) обозначено точкой — это значит, что вектор \(\mathbf B\) направлен перпендикулярно плоскости чертежа к нам.
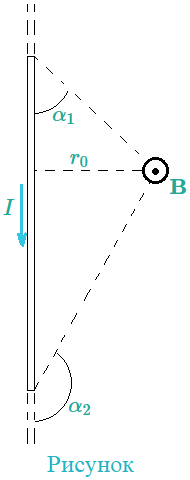
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция, \(\alpha_2=\pi-\alpha_1 \quad и \quad -cos\alpha_2=cos\alpha_1=cos\alpha\), тогда $$B={{\mu\mu_0}\over{2\pi}}{I\over{r_0}} cos \alpha.$$
Магнитная индукция поля соленоида $$B=\mu\mu_0 nI,$$где \(n\) — отношение числа витков соленоида к его длине.
Сила, действующая на прямолинейный проводник с током в магнитном поле (закон Ампера),$$\mathbf F =I[\mathbf l, \mathbf B], \qquad или \qquad F=IBlsin\alpha, $$где \(l\) — длина провода; \(\alpha\) — угол между направлением тока в проводе и вектором магнитной индукции \(\mathbf B\).
Магнитный момент плоского контура с током$$ \mathbf p_m= \mathbf n IS,$$где \(\mathbf n\) — единичный вектор нормали (положительной) к плоскости контура; \(I\) — сила тока, протекающего по контуру; \(S\) — площадь контура.
Формула для механического вращательного момента, действующего на контур с током в магнитном поле,$$ \mathbf M= [\mathbf p_m, \mathbf B], \qquad или \qquad M=p_mBsin\alpha,$$где \(\alpha\) — угол между векторами \( \mathbf p_m\) и \(\mathbf B\).
Потенциальная энергия (механическая) контура с током в магнитном поле$$\Pi_{мех}=-\left(\mathbf p_m, \mathbf B\right), \qquad или \qquad \Pi_{мех}=- p_m B cos \alpha.$$
Отношение магнитного момента \(p_m\) к механическому \(L\) (моменту импульса) заряженной частицы, движущейся по круглой орбите, $${{p_m}\over L}=\frac12 \frac Qm,$$где \(Q\) — заряд частицы; \(m\) —масса частицы.
Сила Лоренца $$\mathbf F=Q[\mathbf v, \mathbf B], \qquad или \qquad F=QvBsin\alpha,$$где \(\mathbf v\) — скорость заряженной частицы; \(\alpha\) — угол между векторами \(\mathbf v\) и \(\mathbf B\).
Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение $$\mathbf F=Q \mathbf E + Q[\mathbf v, \mathbf B].$$
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности $$\Phi=BScos\alpha, \qquad или \qquad \Phi=B_n S,$$где \(S\) — площадь контура; \(\alpha\) — угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности $$\Phi=\int_S B_ndS$$ (интегрирование ведётся по всей поверхности).
Потокосцепление (полный поток) $$\Psi=N\Phi.$$
Работа по перемещению замкнутого контура в магнитном поле $$A=I\Delta\Phi.$$ ЭДС индукции $$\mathscr E=-{{d\Psi}\over{dt}}.$$ Разность потенциалов на концах провода, движущегося со скоростью \(\mathbf v\) в магнитном поле, $$U=Blvsin\alpha,$$где \(l\) — длина провода; \(\alpha\) — угол между векторами \(\mathbf v\) и \(\mathbf B\).
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур, $$Q={{\Delta\Phi}\over R}, \qquad или \qquad Q={{N \Delta\Phi}\over R}={{\Delta\Psi}\over R},$$где \(R\) — сопротивление контура.
Индуктивность контура $$L=\frac \Phi I.$$ ЭДС самоиндукции $$L=\mathscr E_s=-L {{dI}\over{dt}}.$$
Индуктивность соленоида $$L=\mu \mu_0 n^2 V,$$где \(n\) — отношение числа витков соленоида к его длине; \(V\) — объём соленоида.
Мгновенное значение силы тока в цепи, обладающей сопротивлением \(R\) и индуктивностью \(L\):
а) \( \quad I={{\mathscr E}\over R} \left(1-e^{-Rt/L}\right) \quad\) (при замыкании цепи), где \(\mathscr E \) — ЭДС источника тока; \(t\) — время, прошедшее после замыкания цепи;
б) \( \quad I=I_0 e^{-Rt/L} \quad\) (при размыкании цепи), где \(I_0 \) — сила тока в цепи при \(t=0; \; t\) — время, прошедшее c момента размыкания цепи.
Формула для энергии магнитного поля $$W={{LI^2}\over 2}.$$ Объёмная плотность энергии магнитного поля $$w={{BH}\over 2}, \qquad или \qquad w={{B^2}\over {2\mu \mu_0}}, \qquad или \qquad w={{\mu \mu_0 H^2}\over 2},$$где \(B\) — магнитная индукция; \(B\) — напряжённость магнитного поля.
Скорость света в среде$$v=\frac cn,$$где \(c\) — скорость света в вакууме; \(n\) — показатель преломления среды.
Оптическая длина пути световой волны $$L=nl,$$где \(l\) — геометрическая длина пути световой волны в среде с показателем преломления \(n\).
Оптическая разность хода двух световых волн$$\Delta =L_1-L_2.$$
Зависимость разности фаз от оптической разности хода световых волн$$\Delta \varphi =2\pi\left(\frac \Delta \lambda \right),$$где \(\lambda\) — длина световой волны.
Условие макисмального усиления света при интерференции$$\Delta =\pm k\lambda \qquad (k=0, 1, 2,...)$$
Условие максимального ослабления света$$\Delta=\pm(2k+1)\frac \lambda 2.$$
Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой плёнки,$$\Delta=2d\sqrt{n^2-sin^2i_1}\pm \frac \lambda 2,$$или$$\Delta=2dncos i_2 \pm \frac \lambda 2,$$где \(d\) — толщина плёнки; \(n\) — показатель преломления плёнки; \(i_1\) — угол падения; \(i_2\) — угол преломления света в плёнке.
Радиус светлых колец Ньютона в отражённом свете$$r_k=\sqrt{(2k-1)R\lambda/2} \qquad (k=1, 2, 3, ...),$$где \(k\) — номер кольца; \(R\) — радиус кривизны линзы. Радиус тёмных колец Ньютона в отражённом свете$$r_k=\sqrt{kR\lambda}.$$
Угол \(\varphi\) отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия$$a sin \varphi = (2k+1)\lambda/2 \qquad (k=0, 1, 2, 3, ...),$$где \(a\) — ширина щели; \(k\) — порядковый номер максимума.
Угол \(\varphi\) отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции света на дифракционной решётке, определяется из условия$$d sin \varphi = \pm k\lambda \qquad (k=0, 1, 2, 3, ...),$$где \(d\) — период дифракционной решётки.
Разрешающая способность дифракционной решётки$$R=\lambda /\Delta \lambda=kN,$$где \(\Delta \lambda\) — наименьшая разность длин волн двух соседних спектральных линий \((\lambda \; и \; \lambda+\Delta \lambda)\), при которых эти линии могут быть видны раздельно в спектре, полученном посредством данной решётки; \(N\) — полное число щелей решётки.
Формула Вульфа–Брэггов$$2dsin\theta=k\lambda,$$где \(\theta\) — угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); \(d\) — расстояние между атомными плоскостями кристалла.
Закон Брюстера$$tg\varepsilon_B=n_{21},$$где \(\varepsilon_B\) — угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; \(n_{21}\) — относительный показатель преломления второй среды относительно первой.
Закон Малюса$$I=I_0cos^2\alpha,$$где \(I_0\) — интенсивность плоскополяризованного света, падающего на анализатор; \(I\) — интенсивность этого света после анализатора; \(\alpha\) — угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора.
Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
а) \(\varphi=\alpha d\) (в твёрдых телах),
где \(\alpha\) — постоянная вращения; \(d\) — длина пути, пройденного светом в оптически активном веществе;
б) \(\varphi=[\alpha] \rho d\) (в растворах),
где \([\alpha]\) — удельное вращение; \(\rho\) — массовая концентрация оптически активного вещества в растворе.
Релятивистская масса$$m={{m_0}\over{\sqrt{1-(v/c)^2}}}, \qquad или \qquad m={{m_0}\over{\sqrt{1-\beta^2}}},$$где \(m_0\) — масса покоя частицы; \(v\) — её скорость; \(c\) — скорость света в вакууме; \(\beta\) — скорость частицы, выраженная в долях скорости света в вакууме \( ( \beta=v/c)\).
Взаимосвязь массы и энергии релятивистской частицы$$ E=mc^2, \qquad или \qquad E={{m_0 c^2} \over {{\sqrt{1-\beta^2}}}}={{E_0}\over{\sqrt{1-\beta^2}}},$$где \(E_0=m_0c^2\) — энергия покоя частицы.
Полная энергия свободной частицы \(\quad E=E_0+T, \quad \) где \(\;T\) — кинетическая энергия релятивистской частицы.
Кинетическая энергия релятивистской частицы$$T=\left(m-m_0\right)c^2, \qquad или \qquad T=E_0\left({1\over {\sqrt{1-\beta^2}}}-1\right).$$
Импульс релятивистской частицы$$p={{m_0v}\over \sqrt{1-(v/c)^2}}, \qquad или \qquad p=m_0c{\beta \over {1-\beta^2}}.$$
Формула по физике, устанавливающая связь между полной энергией и импульсом релятивистской частицы$$E^2=E_0^2+(pc)^2.$$
Закон Стефана–Больцмана$$R_e=\sigma T^4,$$где \(R_e\) — энергетическая светимость (излучательность) абсолютно чёрного тела; \(\sigma\) — постоянная Стефана–Больцмана; \(T\) — термодинамическая температура Кельвина.
Закон смещения Вина$$\lambda_m=\frac bT,$$где \(\lambda_m\) — длина волны, на которую приходится максимум энергиии излучения; \(b\) — постоянная Вина.
Энергия фотона$$\varepsilon=h\nu, \qquad или \qquad \varepsilon=\hbar \omega,$$где \(h\) — постоянная Макса Планка; \(\hbar=h/2\pi\) — постоянная Планка, делённая на \(2\pi\); \(\nu\) — частота фотона; \(\omega\) — циклическая частота.
Масса фотона$$m={\varepsilon \over {c^2}}={h\over{c\lambda}},$$где \(c\) — скорость света в вакууме; \(\lambda\) — длина волны фотона.
Физическое уравнение для импульса фотона $$p=mc=\frac h \lambda.$$
Формула фотоэффекта$$h\nu=A+T_{max}=A+{{mv_{max}^2}\over 2},$$где \(h\nu\) — энергия фотона, падающего на поверхность металла; \(A\) — работа выхода электрона; \(T_{max}\) — максимальная кинетическая энергия фотоэлектрона.
Красная граница фотоэффекта$$\nu_0 = \frac A h , \qquad или \qquad \lambda_0 = {{hc} \over A},$$где \(\nu_0\) — минимальная частота света, при которой ещё возможен фотоэффект; \(\lambda_0\) — максимальная длина волны света, при которой ещё возможен фотоэффект; \(h\) — постоянная Планка; \(c\) — скорость света в вакууме.
Формула Комптона$$\Delta \lambda=\lambda'-\lambda={h\over {m_0c}}(1-cos \theta),$$или$$\Delta \lambda=\lambda'-\lambda=2{h\over {m_0c}}sin^2 \frac \theta 2),$$где \(\lambda\) — длина волны фотона, встретившегося со свободным или слабосвязанным элетроном; \(\lambda'\) — длина волны фотона, рассеянного на угол \(\theta\) после столкновения с электроном;
Комптоновская длина волны$$\Lambda={h\over{m_0c}} \qquad (\Lambda=2,436 нм).$$
Давление света при нормальном падении на поверхность$$p=E_e(1+\rho)/c=w(1+\rho),$$где \(E_e\) — энергетическая освещённость (облучённость); \(w\) — объёмная плотность энергии излучения; \(\rho\) — коэффициент отражения.
Давление света, падающего под некоторым углом$$p=n_0h\nu(1+\rho)cos^2i,$$ $$p=\lt w \gt(1+\rho)cos^2i,$$ где \(n_0\) — концентрация фотонов падающего света; \(\nu\) — частота падающего света; \(i\) — угол падения, образованный падающим лучом с нормалью к поверхности падения; \(\lt w \gt\) — среднее значение объёмной плотности энергии.
Атомная физика, квантовая механика и физика твёрдого тела
Боровская теория водородоподобного атома. Момент импульса электрона (второй постулат Бора)$$L_n=\hbar n \qquad или \qquad mv_nr_n=\hbar n,$$где \(m\) — масса электрона; \(v_n\) — скорость электрона на \(n\)-ой орбите; \(r_n\) — радиус \(n\)-ой стационарной орбиты; \(\hbar\) — постоянная Планка \(\left(\hbar=6,63\cdot10^{-34}Дж;\cdot с\right)\); \(n\) — главное квантовое число (n=1,2,3,...).
Радиус \(n\)-ой стационарной орбиты $$r_n=a_0n^2,$$где \(a_0\) — первый боровский радиус.
Энергия электрона в атоме водорода $$E_n=E_i/n^2,$$где \(E_i\) — энергия ионизации атома водорода.
Энергия, излучаемая или поглощаемая атомом водорода, $$\varepsilon=\hbar \omega =E_{n_2}-E_{n_1},$$или
$$\varepsilon = E_i \left( {1 \over {n_1^2}}-{1 \over {n_2^2}} \right) ,$$где \(n_1\) и \(n_2\) — квантовые числа, соответсвующие энергетическим уровням, между которыми совершается переход электрона в атоме.
Спектроскопическое волновое число $$\tilde \nu=\frac 1 \lambda = R \left( {1 \over {n_1^2}}-{1 \over {n_2^2}} \right),$$где \(\lambda\) — длина волны излучения или поглощения атомом; \(R\) — постоянная Ридберга \(\left(R=1,1 \cdot 10^7 м^{-1}\right)\).
Формулы по физике, выражающие волновые свойства частиц. Длина волны де Бройля$$\lambda={{2\pi\hbar}\over p},$$где \(p\) — импульс частицы.
Импульс частицы и его связь с кинетической энергией \(T\): $$ a) \quad p=m_o v;\quad p=\sqrt{2 m_0 T}; \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad $$ $$ б) \quad p=m v={{m_0 v} \over {\sqrt{1-\left({\frac v c}\right)^2}}};\quad p=\frac 1 c \sqrt{\left(2E_0+ T\right)T} \; , \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad $$где \(m_0\) — масса покоя частицы; \(m\) — релятивистская масса частицы; \(v\) — скорость частицы; \(с\) — скорость света в вакууме; \(E_0\) — энергия покоя частицы \(\left(E_0=m_0c^2\right)\).
Соотношение неопределённостей:
а) \(\Delta p_x \Delta x \ge \hbar \) (для координаты и импульса),
где \(\Delta p_x\) — неопределённость проекции импульсяа на ось \(X\); \( \Delta x \) — неопределённость координаты;
б) \(\Delta E \Delta t \ge \hbar \) (для энергии и времени),
где \(\Delta\) — неопределённость энергии; \(\Delta t \) — время жизни квантовой частицы в данном энергетическом состоянии.
Одномерное уравнение Шредингера для стационарных состояний$${{d^2\psi}\over{dx^2}}+{{2m}\over{\hbar^2}}(E-U)\psi(x)=0,$$где \(\psi(x)\) — волновая функция, описывающая состояние частицы; \(m\) — масса частицы; \(E\) — полная энергия; \(U=U(x)\) — потенциальная энергия частицы.
Плотность вероятности$${{dw(x)}\over{dx}}=|\psi(x)|^2,$$где \(dw(x)\) — вероятность того, что частица может быть обнаружена вблизи точки с координатой \(x\) на участке \(dx\).
Вероятность обнаружения частицы в интервале от \(x_1\) до \(x_2\)$$w=\int_{x_1}^{x_2}|\psi(x)|^2dx.$$
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:
а) \(\psi_n(x)=\sqrt{\frac 2l}sin{{\pi n}\over l}x\) (собственная нормированная волновая функция);
б) \(E_n={{\pi^2 \hbar^2 n^2}\over{2ml^2}}\) (собственное значение энергии),
где \(n\) квантовое число (\(n=1, 2, 3,...) \); \(l\) — ширина ящика. В области \(0 \le x \le l, U=\infty\) и \(\psi(x)=0.\)
Атомное ядро. Радиоактивность. Массовое число ядра (число нуклонов в ядре)$$A=Z+N,$$где \(Z\) — зарядовое число (число протонова); \(N\) — число нейтронов.
Физический закон радоактивного распада $$dN=-\lambda N dt, \qquad или \qquad N=N_0e^{-\lambda t }$$где \(dN\) — число ядер, распадающихся за интервал времени \(dt\); \(N\) — число ядер, не распавшихся к моменту времени \(t\); \(N_0\) — число ядер в начальный момент времени (\(t=0\)); \(\lambda\) — постоянная радиоактивного распада.
Число ядер, распавшихся за время \(t\),$$\Delta N=N_0-N=N_0\left(1-e^{-\lambda t}\right).$$
Зависимость периода полураспада от постоянной радиоактивного распада$$T_{1/2}={{ln2}\over{\lambda}}={{0,693}\over{\lambda}}.$$
Среднее время \(\tau\) жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшается в \(e\) раз,$$\tau=\frac 1 \lambda.$$
Число \(N\) атомов, содержащихся в радиоактивном изотопе, $$N={{mN_A}\over \mu},$$где \(m\) — масса изотопа; \(\mu\) — молярная масса; \(N_A\) — постоянная Авогадро.
Формула для активности \(A\) радиоактивного изотопа$$A=-{{dN}\over{dt}}=\lambda N, \qquad или \qquad A=\lambda N_0 e^{-\lambda t}=A_0e^{-\lambda t},$$где \(dN\) — число ядер, распадающихся за интервал времени \(dt\); \(A_0\) — активность изотопа в начальный момент времени.
Удельная активность изотопа \(a=A/m\).
Дефект массы ядра$$\Delta m =Zm_p+(A-Z)m_n-m_я,$$где \(Z\) — зарядовое число (число протонов в ядре); \(A\) — массовое число (число нуклонов в ядре); (\(A-Z\)) — число нейтронов в ядре; \(m_p\) — масса протона; \(m_n\) — масса нейтрона; \(m_я\) — масса ядра.
Энергия связи ядра$$E_{св}=\Delta mc^2,$$где \(\Delta m\) — дефект масс ядра; \(c\) — скорость света в вакууме.
Теплоёмкость кристалла. Средняя энергия квантового одномерного осциллятора$$\left< \varepsilon \right>=\varepsilon_0+{{\hbar \omega}\over {e^{\hbar \omega/kT}-1}},$$где \(\varepsilon_0\) — нулевая энергия \(\left(\varepsilon_0=\hbar \omega/2\right)\); \(\hbar\) — постоянная Планка; \(\omega\) — круговая частота колебаний осциллятора; \(k\) — постоянная Больцмана; \(T\) — термодинамическая температура.
Формула по физике для молярной внутренней энергии системы, состоящей из невзаимодействующих квантовых осциляторов,$$U_m=U_{0m}+{{3R\Theta_E}\over{e^{\Theta_E/T}-1}},$$где \(R\) — молярная газовая постоянная; \(\Theta_E=\hbar \omega /k\) — характеристическая температура Эйнштейна; \(U_{0m}=\)⅔\(R\Theta_E\) — молярная нулевая энергия (по Эйнштейну).
Молярная теплоёмкость кристаллического твёрдого тела в области низких температур (предельный закон Дебая)$$C_m={{12\pi^4}\over 5}R\left({T\over {\Theta_D}}\right)^3=234R\left({T\over {\Theta_D}}\right)^3 \qquad \left( T \ll \Theta_D \right).$$
Теплота, необходимая для нагревания тела,$$Q=\frac mM \int_{T_1}^{T_2}C_mdT,$$где \(m\) — масса тела; \(mu\) — молярная масса; \(T_1\) и \(T_2\) — начальная и конечная температура тела.
Элементы квантовой статистики. Распределение свободных электронов в металле по энергиям при \(0К\)$$dn(\varepsilon)={1 \over {2\pi^2}} \left({{2m} \over {\hbar^2}}\right)^{3/2}\varepsilon^{1/2}d\varepsilon,$$где \(dn(\varepsilon)\) — концентрация электронов, энергия которых заключена в пределах от \(\varepsilon\) до \(\varepsilon+d\varepsilon\); \(m\) — масса электрона. Это выражение справедливо при \(\varepsilon \lt \varepsilon_F\) (где \(\varepsilon_F\) — энергия или уровень Ферми).
Энергия Ферми в металле при \(T=0 К\)$$\varepsilon_F={{\hbar^2}\over {2m}}\left(3\pi^2n\right)^{2/3},$$где \(n\) — концентрация электронов в металле.
Полупроводники. Удельная проводимость собственных полупроводников$$\gamma=\gamma_0exp\left(-{{\Delta E}\over {2kT}}\right),$$где \(\Delta E\) — ширина запрещённой зоны; \(\gamma_0\) — константа.
Сила тока в \(p-n\)–переходе$$I=I_0\left[exp\left({{eU}\over{kT}}\right)-1\right],$$где \(I_0\) — предельное значение силы обратного тока; \(U\) — внешнее напряжение, приложенное к \(p-n\)–переходу.
Контактные и термоэлектрические явления. Внутренняя контактная разность потенциалов $$U_{12}={{\varepsilon_{F_1}-\varepsilon_{F_2}}\over e},$$где \(\varepsilon_{F_1}\) и \(\varepsilon_{F_2}\) — энергия Ферми соответственно для первого и второго металлов; \(e\) — заряд электрона.