


Колебания есть движения, повторяющиеся со временем. Колеблющиеся системы называются маятниками. Маятник — это система совершающая колебания — колеблющаяся система. Для возникновения колебаний необходимо, чтобы при отклонении системы от положения равновесия, равнодействующая возникающих сил возвращала систему в исходное положение равновесия, и чтобы трение отсутствовало или было достаточно мало. Такими колеблющимися системами или маятниками, например, являются: математический маятник; физический маятник; пружинный маятник; крутильный маятник; колебательный контур; груз, скользящий в полусфере; буй, колеблющийся в тихой воде; стержень, лежащий на цилиндрической поверхности.
Математический маятник представляет собой груз, подвешенный на длинной нити. Его также называют нитяной маятник.
Физический маятник — это некое твёрдое тело, шарнирно закреплённое в одной точке и могущее совершать колебания.
Пружинный маятник представляет собой груз, прикреплённый к пружине.
Крутильный маятник — груз на длинной нити. В отличие от математического маятника, крутильный маятник не раскачивается, а закручивается и раскручивается.
Груз, скользящий по внутренней поверхности полусферы, тоже совершает колебания и при малом трении ведёт себя как маятник. Стержень, раскачивающийся на цилиндрической поверхности, обладает признаками маятника.
Буй на спокойной ровной воде теоретически тоже может рассматриваться как маятник.
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят электромагнитные колебания.
Для возникновения колебаний необходимо, чтобы при отклонении системы от положения равновесия, равнодействующая возникающих сил возвращала систему в исходное положение равновесия, и чтобы трение отсутствовало или было достаточно мало. Возвращающую силу называют также восстанавливающей силой. Смотрите, например, решение задач по физике.
При отсутствии трения и сопротивления движению колебания маятника подчиняются однородному линейному дифференциальному уравнению второго порядка$$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ddot x + \omega^2 x = 0 . \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)$$Величина \( \omega \) называется циклической частотой колебаний.
Функция$$x(t)=Bcos \omega t+Csin \omega t$$является решением дифференциального уравнения (1) при любых значения параметров \(B\) и \(C\). Действительно, продифференцируем дважды функцию \(x(t)\) по времени \(t\).$$\dot x(t)=-B \omega sin \omega t+C \omega cos \omega t \, ,$$$$\ddot x (t)=-B \omega^2 cos \omega t-C \omega^2 sin \omega t \, .$$Подставим \( x(t) \) и \( \ddot x (t) \) в уравнение (1). Получим$$\ddot x + \omega^2 x=-B\omega^2 cos \omega t-C \omega^2 sin \omega t+\omega^2 (B cos \omega t+Csin \omega t)=0 \, .$$Что и требовалось показать.
Параметры \(B\) и \(C\) подбираются исходя из начальных условий. Например, если в начальный момент колеблющаяся величина \(x\) равна нулю, а скорость её изменения не нулевая, то колебания будут происходить по закону синуса. Действительно, подставим в уравнение \(t=0\), \(x=0\). Получим$$x(0)=Bcos0+Csin0=0 \, . $$Отсюда \(B=0\) и уравнение колебаний запишется$$x(t)=Csin \omega t \, . $$
Если в начальный момент нулю равна скорость изменения колеблющейся величины, то есть её производная, а сама изменяющаяся величина не равна нулю, а равна, например, \(x_0\), то колебания будут происходить по закону косинуса. Действительно, подставим выражение для \(x(t)\) в эти начальные условия$$x(0)=Bcos0+Csin0=B=x_0 \, ,$$$$\dot x (0)=-B \omega sin0+C \omega cos0=C \omega =0 \, .$$Отсюда \( B=x_0 \) и \( C=0 \). Тогда$$x(t)=x_0 cos\omega t.$$
Такие колебания, происходящие по закону синуса или косинуса, называются гармоническими колебаниями. Дифференциальное уравнение (1) называется дифференциальным уравнением гармонических колебаний.
Так как максимальные значение синуса и косинуса равны единице, то максимальное отклонение, называемое амплитудой, равно
$$x_{max} = C \cdot 1 = C \, ,$$$$x_{max} = x_0 \, .$$Таким образом, \(C =x_{max} \).
Амплитуда колебаний обозначается буквой \(A\). Следовательно, \(A=C=x_{max} \).
Максимальная скорость при этом равна$$v_{max}=A \omega \, .$$Действительно, например, для случая колебаний по закону синуса$$x(t)=Asin \omega t \,$$скорость$$v(t)={{dx} \over {dt}} = \dot x = A \omega cos \omega t \, .$$Максимальная скорость будет когда косинус равен единице, то есть \( v_{max}=A \omega \) . Что и требовалось показать.
Аналогично проверяется для колебаний, происходящих по закону косинуса.
В начальный момент \( v(0)=v_0 \). Следовательно, \(A \omega cos0=A \omega =v_0 \) .
Максимальное отклонение от положения равновесия$$x_{max} =A= {{v_0} \over \omega } \, .$$
Ускорение$$a(t)={{dv(t)} \omega {dt} } = \dot v = -A \omega^2 sin \omega t \, .$$
Максимальное ускорение$$a_{max}=A \omega^2 \, .$$ На рисунке 1 изображён график зависимости угла отклонения от положения равновесия при колебаниях, происходящих по закону косинуса.
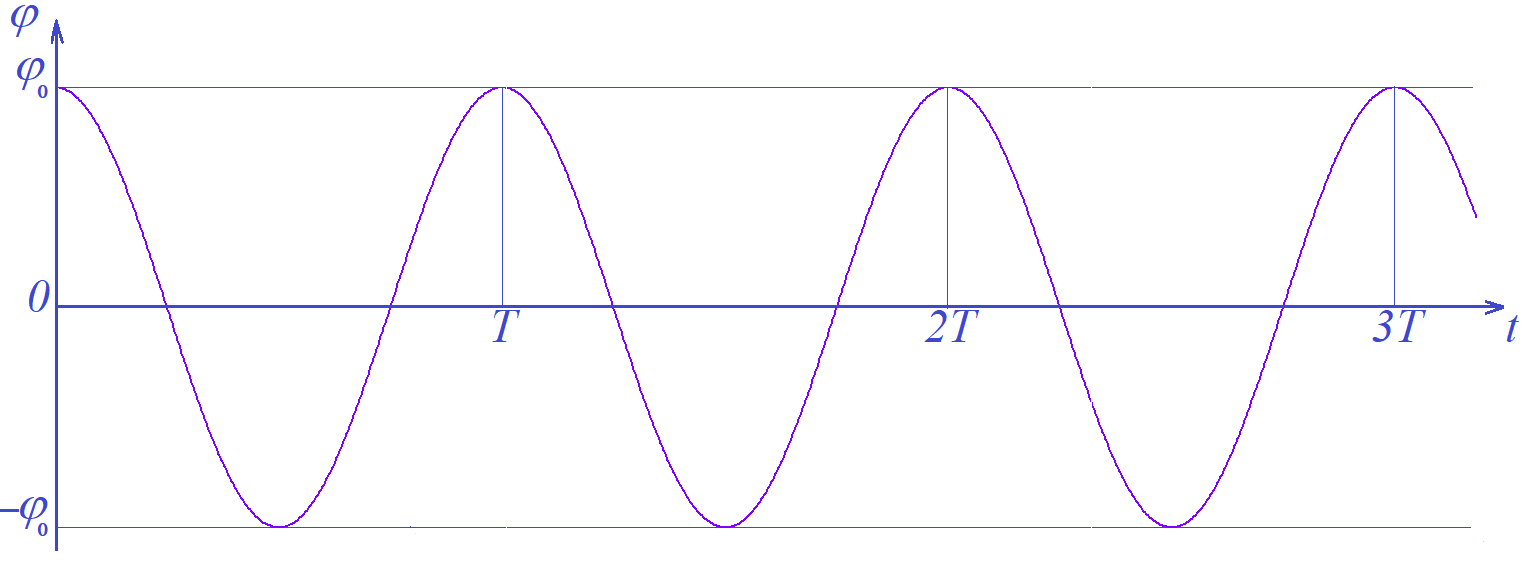
Рисунок 1.
На рисунке 2 изображён график зависимости отклонения от положения равновесия при колебаниях, происходящих по закону синуса.
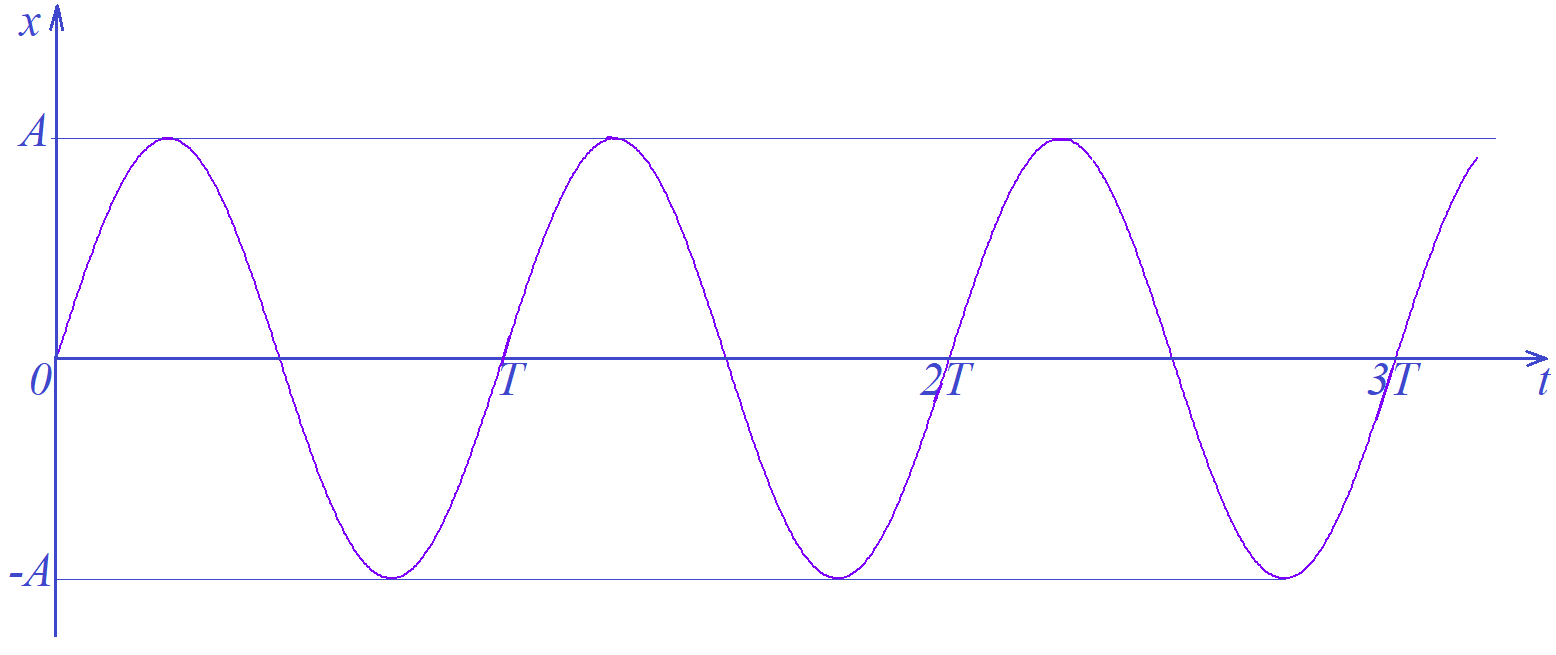
Рисунок 2.
Синус, как и косинус, является периодической функцией с периодом \( 2 \pi \) , так как$$sin( \alpha +2 \pi )=sin( \alpha ) \, .$$
Функция \( f(t) \) есть периодическая функция с периодом \(T\), если для любого значения аргумента \(t\) справедливо равенство$$f(t+T)=f(t) \, .$$
Применим данное определение для полученного уравнения колебаний$$x(t+T)=Asin( \omega (t+T))=x(T)=Asin( \omega t) \, .$$Отсюда$$Asin( \omega (t+T))=Asin( \omega t) \, ,$$или$$sin( \omega t+ \omega T))= sin( \omega t) \, .$$
Так как период синуса равен \( 2 \pi \), то из последнего равенства получаем$$\omega T=2 \pi \, ,$$или$$T={{2 \pi } \over \omega } \, .$$
Период колебаний — это время, за которое совершается одно полное колебание, при котором груз возвращается в исходное положение.
Частота колебаний — это число колебаний, совершаемых маятником за одну секунду. Частота колебаний равна$$\nu = { 1 \over T} ={ \omega \over {2 \pi }} \, .$$Из последнего равенства можем записать выражение для циклической частоты$$\omega = 2 \pi \nu = { {2 \pi } \over T} \, .$$
У каждого маятника своя циклическая частота, зависящая от его геометрических и физических параметров.
Циклическая частота колебаний математического маятника равна$$\omega = \sqrt {g \over l} \, ,$$где \(g\) — ускорение свободного падения, \(l\) — длина нити подвеса.
Циклическая частота колебаний физического маятника равна$$\omega = \sqrt {{mga} \over J} \, ,$$где \(m\) — масса маятника, \(J\) — момент инерции груза маятника относительно точки подвеса, \(a\) — расстояние от точки подвеса до центра масс.
Циклическая частота колебаний пружинного маятника равна$$\omega = \sqrt {k \over m} \, ,$$где \(m\) — масса груза маятника, \(k\) — жёсткость пружины маятника.
Циклическая частота колебаний крутильного маятника равна$$\omega = \sqrt {{GJ_p} \over {Jl}} \, ,$$где \(G\) — модуль сдвига материала упругой нити, \(J_p\) — полярный момент инерции поперечного сечения нити, \(J\) — момент инерции груза, \(l\) — длина нити.
Циклическая частота колебаний груза, скользящего по внутренней поверхности полусферы, равна$$\omega = \sqrt {g \over R} \, ,$$где \(R\) — радиус полусферы.
Циклическая частота колебаний стержня, качающегося на цилиндрической поверхности, равна$$\omega = {2 \over l} \sqrt {3gR} \, ,$$где \(l\) — длина стержня, \(R\) — радиус кривизны поверхности.
Циклическая частота колебаний буя на поверхности воды$$\omega = \sqrt {{ \rho g S } \over m} \, ,$$где \(rho = 1 г/см^3 \) — плотность воды, \(S\) — площадь поперечного сечения цилиндрического буя, \(m\) — масса буя.
Циклическая частота электромагнитных колебаний в колебательном контуре равна$$\omega = { 1\over {\sqrt {LC }}} \, ,$$где \(L \) — индуктивность катушки, а \(C \) — электроёмкость конденсатора.
Соответственно, период колебаний маятника также зависит от геометрических и физических параметров маятника.
Период колебаний математического маятника$$T = 2 \pi \cdot \sqrt { l \over g } \, .$$
Физический маятник имеет период колебаний$$T = 2 \pi \cdot \sqrt { J \over {mga} } \, .$$
Период колебаний пружинного маятника$$T = 2 \pi \cdot \sqrt { m \over k } \, .$$
Период колебаний стержня на цилиндре$$T = {{\pi l} \over \sqrt {3gR}} \, .$$
Период колебаний буя (поплавка)$$T = 2 \pi \cdot \sqrt { m \over {\rho g S} } \, .$$
Период колебаний крутильного маятника$$T = 2 \pi \cdot \sqrt {{Jl} \over {GJ_p} } \, .$$
Период электромагнитных колебаний в колебательном контуре$$T = 2 \pi \cdot \sqrt {LC } \, .$$

Научно-популярные фильмы о колебаниях
| Математический маятник | Физический маятник | Пружинный маятник | Крутильный маятник |
| Колебания груза в полусфере | Колебания стержня на цилиндре | Колебания буя на воде |
