


Математический маятник представляет собой груз массы \(m \), подвешенный на длинной нити длины \(l\)
Рассмотрим колебания маятника с точки зрения второго закона Ньютона и найдём период колебаний математического маятника. На груз действует две силы: сила тяжести \(m \vec g \), направленная вниз, и сила натяжения нити \( \vec F \), направленная вдоль нити от груза. По второму закону Ньютона$$\vec F + m \vec g = m \vec a .$$ Здесь \( \vec a =\vec a_{\tau} + \vec a_n \) — ускорение груза; \( \vec a_{\tau} \) — касательное (тангенциальное) ускорение груза, направленное по касательной к траектории; \( \vec a_n \) —
нормальное (центростремительное) ускорение груза, направленное к центру траектории, то есть вдоль нити.
Проведём оси координат так, как показано на рисунке 1. Тогда второй закон Ньютона в проекции на ось абсцисс:$$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad -mg sin \varphi = m a_{\tau} . \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)$$Здесь \( \varphi \) — угол отклонения нити от вертикали. Положительным направлением угла отклонения считаем направление против часовой стрелки, то есть влево.

Рисунок 1.
В проекции на ось ординат второй закон Ньютона запишется:$$F-mgcos \varphi = m a_n.$$
Касательное ускорение равно$$a_{\tau}=\varepsilon l,$$где \( \varepsilon = \ddot \varphi \) — угловое ускорение, здесь двумя
точками обозначена вторая производная по времени. Подставим в (1) и получим$$-mg sin \varphi = m l \ddot \varphi \, .$$
Полагая, что маятник отклоняется на достаточно малые углы, примем
Обозначим \( \omega = \sqrt {g / l} \). Тогда последнее дифференциальное уравнение перепишется в виде:$$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ddot \varphi + \omega^2 \varphi = 0 \, . \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (2)$$
Как и в предыдущем случае, несложно убедиться, что функция$$\varphi (t)=Bcos \omega t+C sin \omega t$$ является решением уравнения (1) при любых значения величин \(B\) и \(C\). Такое решение называется общим решением
дифференциального уравнения (2).
Для определения произвольных постоянных \(B \) и \(C\) воспользуемся условиями в начале колебаний — начальными условиями. В начальный момент времени, когда
Подставим функцию \( \varphi (t) \) и её производную \( \dot \varphi (t) \) в эти условия. Получим \( B = \varphi_0 \, , C\omega =0 \). Тогда решение$$\varphi (t) = \varphi_0 cos \omega t \, .$$
Мы видим, что колебания происходят по закону косинуса. Последнее уравнение называется уравнением колебаний математического маятника. Колебания, происходящие по закону синуса или косинуса, называются гармоническими колебаниями. На рисунке 2 изображён график зависимости угла отклонения от времени.
Если провести оси координат из положения равновесия, то уравнение колебаний можно переписать в виде:$$x (t) = x_0 cos \omega t \, .$$
Если в начальном положении груз не был отклонён, а ему толчком была придана начальная скорость v_0, уравнение колебаний запишется в виде:$$x (t) = A sin \omega t \, .$$
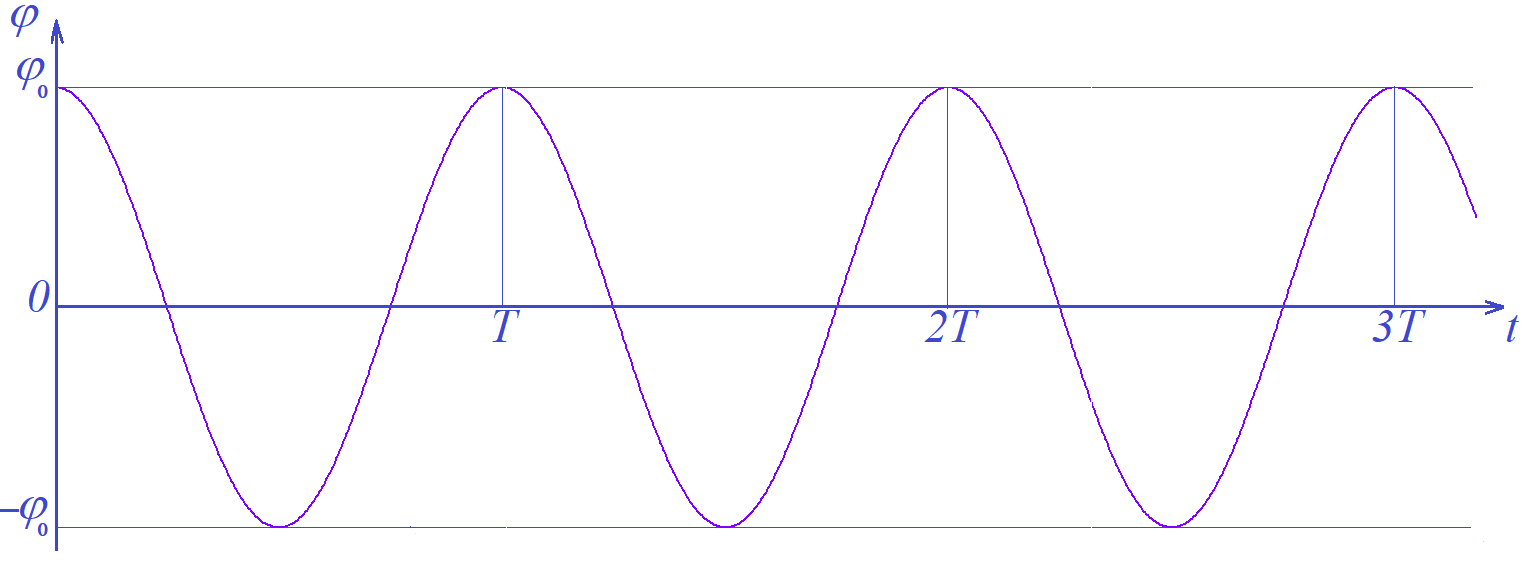
Рисунок 2.
Маятник, точнее его груз, имеет скорость$$v (t) = {{dx} \over{dt}} = \dot x = A \omega cos \omega t \, .$$ Максимальная скорость \( v_{max}=A \omega \, .\)
В начальный момент \( v(0)=v_0 \). Следовательно,
Максимальное отклонение от положения равновесия есть амплитуда колебаний.$$x_{max} =A = {{v_0} \over \omega } \, .$$
Математический маятник, а точнее его груз, имеет ускорение$$a(t) = {{dv(t)} \over{dt}} = \dot v =-A \omega^2 sin \omega t \, .$$ Максимальное ускорение \( a_{max} = A \omega^2 \, . \)
На рисунке 3 изображён график зависимости отклонения от времени при колебаниях, совершаемых по закону синуса.
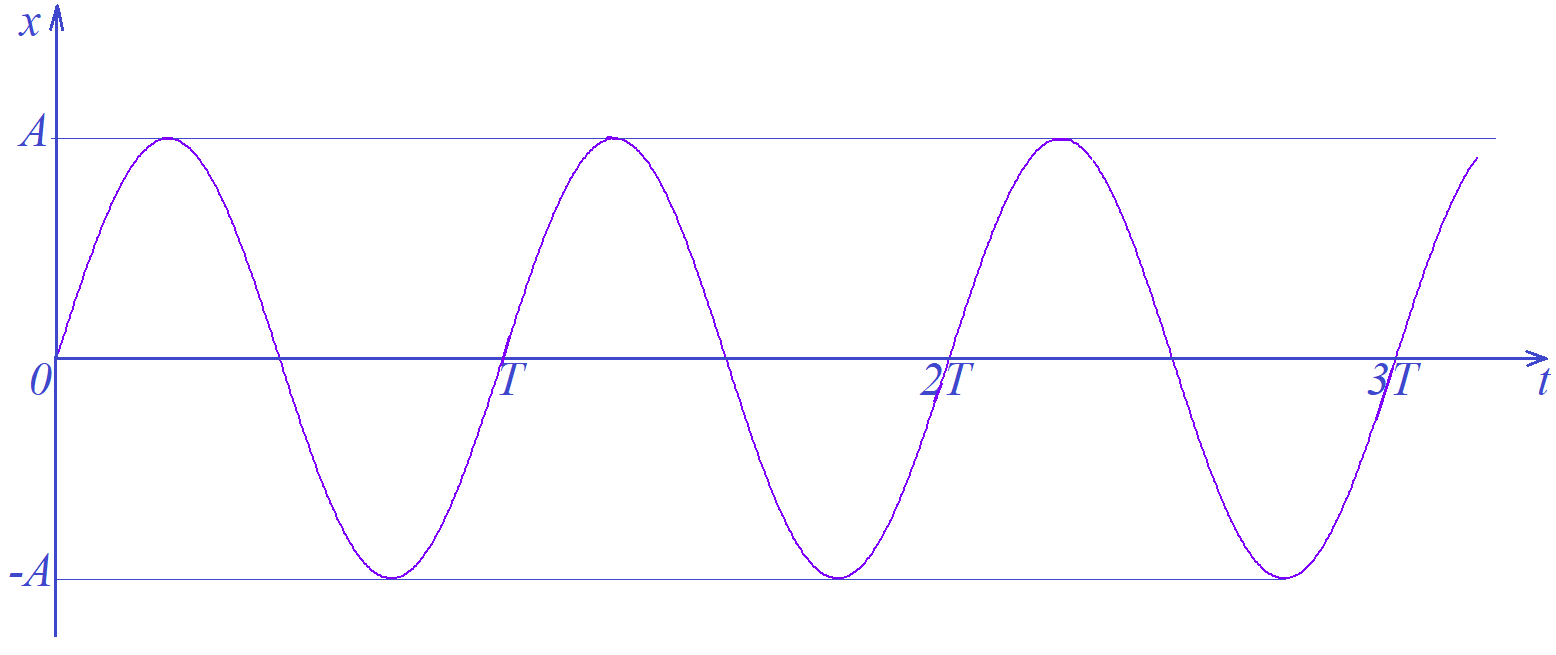
Рисунок 3.
Величина \( \omega = \sqrt {g/l} \), как и ранее, называется циклической частотой колебаний. Как и в предыдущем случае
Период колебаний математического маятника$$T = 2 \pi \cdot \sqrt {g \over l} \, .$$
Частота колебаний маятника — число колебаний маятника за одну секунду — равна
$$\nu = {1 \over T} = {{2 \pi} \over \omega } \, .$$ Отсюда
Равнодействующая сил, приложенных к грузу маятника, называется восстанавливающей или возвращающей силой. По второму закону Ньютона восстанавливающая сила равна
$$F = ma = -A m \omega^2 sin \omega t \, .$$
Максимальное значение возвращающей силы равно$$F_{max} = A m \omega^2 = {{Amg} \over l } \, .$$
Кинетическая энергия груза маятника равна$$E_к = {{mv^2} \over 2} = {{mA^2 \omega^2} \over 2}cos^2 \omega t \, .$$
Полная энергия колебаний маятника, по закону сохранения, равна максимальной кинетической энергии груза маятника
$$E=E_{к \; max} = {{mA^2 \omega^2} \over 2} \, .$$
Потенциальная энергия маятника равна$$E_п = E-E_{к \; max} = {{mA^2 \omega^2} \over 2} sin^2 \omega t \, .$$
| Математический маятник | Физический маятник | Пружинный маятник | Крутильный маятник |
| Колебания груза в полусфере | Колебания стержня на цилиндре | Колебания буя на воде |
