

Бесплатные решения к сборнику заданий
Кузнецова Л. А.
Другие
бесплатные решения
|



 |
ПРИМЕР ПО МАТЕМАТИКЕ

Решение.
Общий член ряда 
Согласно радикальному признаку Коши, ряд сходится абсолютно, если 
то есть, если 
Для определения интервала сходимости получаем неравенство 
или 
Отсюда 
На конце интервала, при  ряд расходится. Следовательно, область сходимости ряда
ряд расходится. Следовательно, область сходимости ряда 
Ответ: Область сходимости ряда 
Найти частное решение дифференциального уравнения
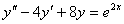 , удовлетворяющее
начальным условиям , удовлетворяющее
начальным условиям 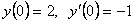 . .
РЕШЕНИЕ
Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение представляет собой сумму общего решения соответствующего однородного уравнения и какого либо частного решения исходного уравнения.
То есть 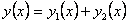 . .
Здесь: 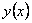 - общее решение исходного уравнения; - общее решение исходного уравнения;
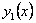 - общее решение соответствующего однородного уравнения - общее решение соответствующего однородного уравнения 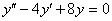 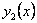 - некоторое частное решение исходного неоднородного уравнения. - некоторое частное решение исходного неоднородного уравнения.
Решим сначала соответствующее однородное уравнение. Для этого решим сначала характеристическое уравнение 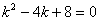 . .
Дискриминант 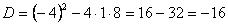 . .
Корни комплексные сопряжённые 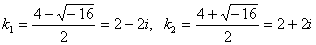 . .
Следовательно, общее решение однородного уравнения 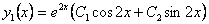 . .
В правой части исходного уравнения стоит функция 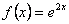 , которую можно представить в виде , которую можно представить в виде 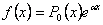 . Здесь . Здесь 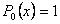 - многочлены нулевой степени (то есть, попросту говоря, числа). - многочлены нулевой степени (то есть, попросту говоря, числа).
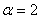 - не является корнем характеристического уравнения. - не является корнем характеристического уравнения.
Поэтому, частное решение исходного уравнения будем искать в виде 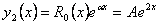
Найдём первую и вторую производные от этого решения и подставим в исходное уравнение.
Первая производная 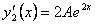 . Вторая производная . Вторая производная 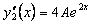
Подставляя в исходное уравнение, получим 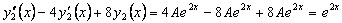 . .
Отсюда 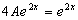 и A=0,25 . и A=0,25 .
Тогда частное решение исходного уравнения будет иметь вид 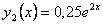 . .
Следовательно, общее решение исходного уравнения будет иметь вид 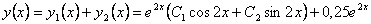 . .
Найдём производную от общего решения 
Для определения произвольных постоянных воспользуемся начальными условиями 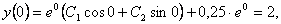 , , 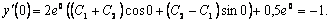 . .
Отсюда 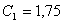 и и 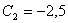 . .
Тогда частное решение, удовлетворяющее начальным, условиям имеет вид 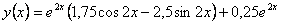 . .
Ответ: Частное решение, удовлетворяющее начальным условиям 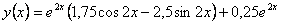 . .
______________________________________________________________________
ПРИМЕРЫ ПО ФИЗИКЕ

Задачи по физике
Задача линейного программирования
Математические методы в экономике
Образцы решения задач по математическим методам в экономике
Решение квадратного уравнения онлайн
Другие бесплатные решения
|
|
|













