
Метод интегрирования дифференцированием
Ответы на экзаменационные вопросы по Высшей математике
|



 |
Задача со вступительного экзамена географака МГУ
Для каждого значения 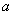 , удовлетворяющего неравенствам , удовлетворяющего неравенствам 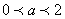 найти наименьшее значение выражения найти наименьшее значение выражения 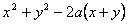 при условии при условии 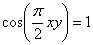 . .
Решение
 ______________________________________________________________________
______________________________________________________________________
ЗАДАЧИ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ МЭИ
Задачи вступительного экзамена по математике.
ВАРИАНТ 1.


ВАРИАНТ 2.


ВАРИАНТ 3.



ВАРИАНТ 4.



А.А. Болотов, В.И. Прохоренко, В.Ф. Сафонов, Задачи из Банка вступительных экзаменов.
Задача № 44. (стр.103)
Периметр остроугольного треугольника ABC равен 16см, площадь треугольника равна 12 кв.см.
Найти длины сторон треугольника АВС, если его углы 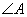 и и 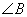 связаны соотношением связаны соотношением 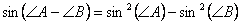
Решение

Задача № 53. (стр.104)
Периметр треугольника равен 18 см, длины a, b, c его сторон удовлетворяют соотношению 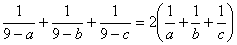 .
Найти площадь треугольника. .
Найти площадь треугольника.
Решение

Назад на страницу БЕСПЛАТНО
НАЙТИ ОБЩЕЕ СОПРОТИВЛЕНИЕ ЦЕПИ

Решение

 ______________________________________________________________________
______________________________________________________________________
Найти ранг матрицы

Решение
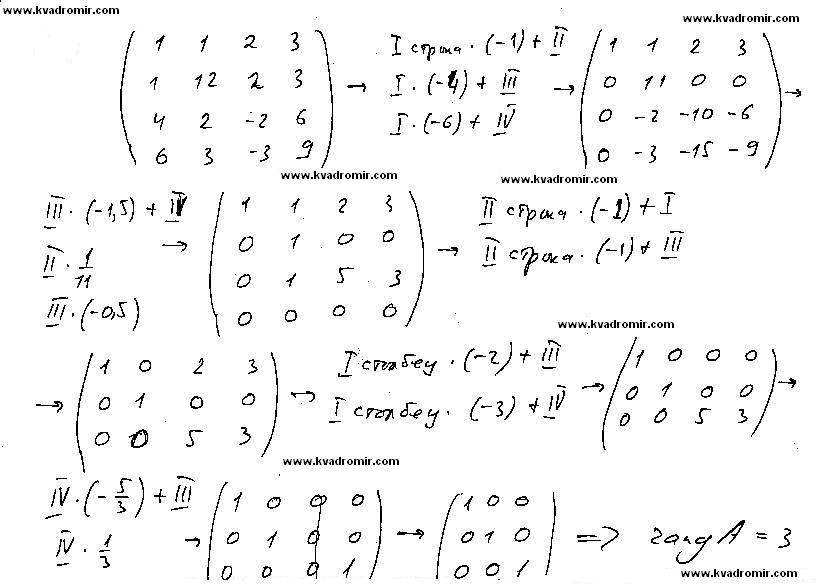
______________________________________________________________________
Задание по векторной алгебре.
Даны векторы 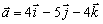 , , 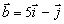 , , 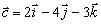
Требуется найти
a) 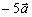 и и 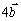 ; ;
b) Скалярное произведение векторов 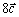 и и 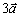 ; ;
с) Выяснить коллинеарны ли векторы  и и 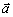 , и являются ли они ортогональными; , и являются ли они ортогональными;
d) Выяснить компланарны ли векторы 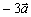 , , 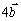 и и 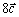
Решение
 ______________________________________________________________________
______________________________________________________________________
ПРЕДЕЛЫ
Найти предел
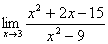
Решение
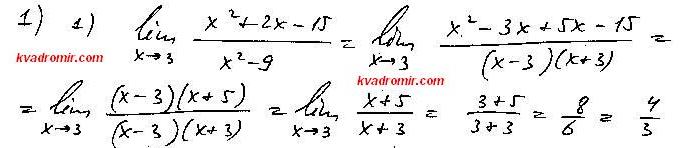 ______________________________________________________________________
______________________________________________________________________
Найти предел
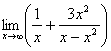
Решение
 _________________________________________________________________________________
_________________________________________________________________________________
Найти предел
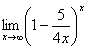
Решение
 _________________________________________________________________________________
_________________________________________________________________________________
Найти предел

Решение
 _________________________________________________________________________________
_________________________________________________________________________________
Вычисление разных пределов
Решение
 _________________________________________________________________________________
_________________________________________________________________________________
ПРОИЗВОДНЫЕ
Найти производную
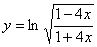
Решение


 ______________________________________________________________________
______________________________________________________________________
ИССЛЕДОВАНИЕ ФУНКЦИЙ
Исследуйте функцию и постройте график
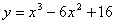
Решение
 ______________________________________________________________________
______________________________________________________________________
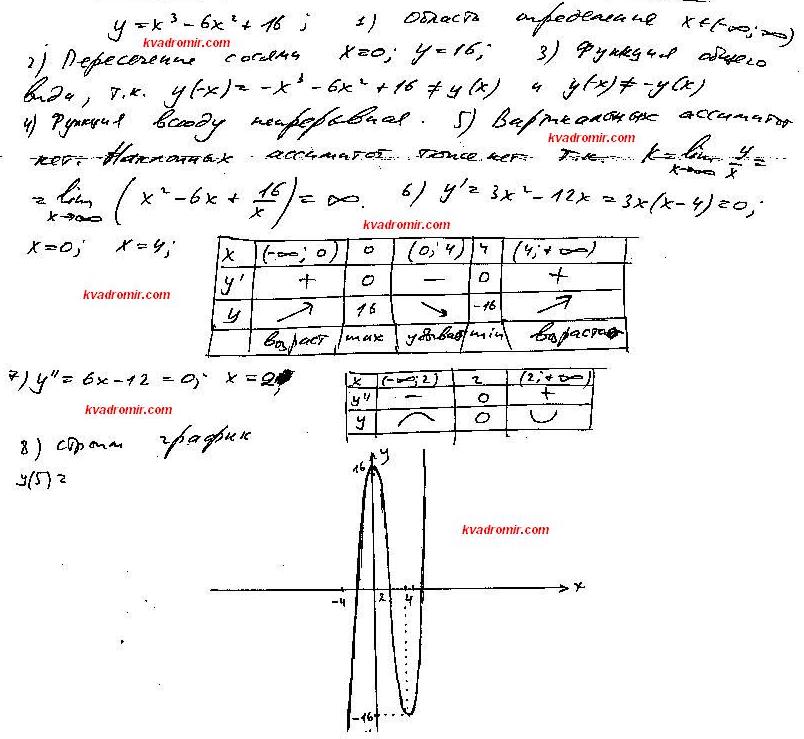
Исследуйте функцию и постройте график
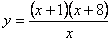
Решение
 ______________________________________________________________________
______________________________________________________________________
Интегралы
Найти неопределённый интеграл
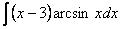
Решение
 ______________________________________________________________________
______________________________________________________________________
Найти неопределённый интеграл
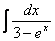
Решение
 _________________________________________________________________________________
_________________________________________________________________________________
Найти неопределённый интеграл
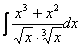
Решение
 _________________________________________________________________________________
_________________________________________________________________________________
Найти неопределённый интеграл
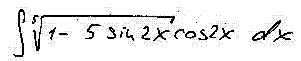
Решение
 ______________________________________________________________________
______________________________________________________________________
Найти неопределённый интеграл
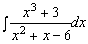
Решение
 ______________________________________________________________________
______________________________________________________________________
Найти неопределённый интеграл
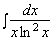
Решение
 ______________________________________________________________________
______________________________________________________________________
Найти неопределённый интеграл
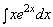
Решение
 ______________________________________________________________________
______________________________________________________________________
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Вычислить определённый интеграл
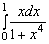
Решение
 ______________________________________________________________________
______________________________________________________________________
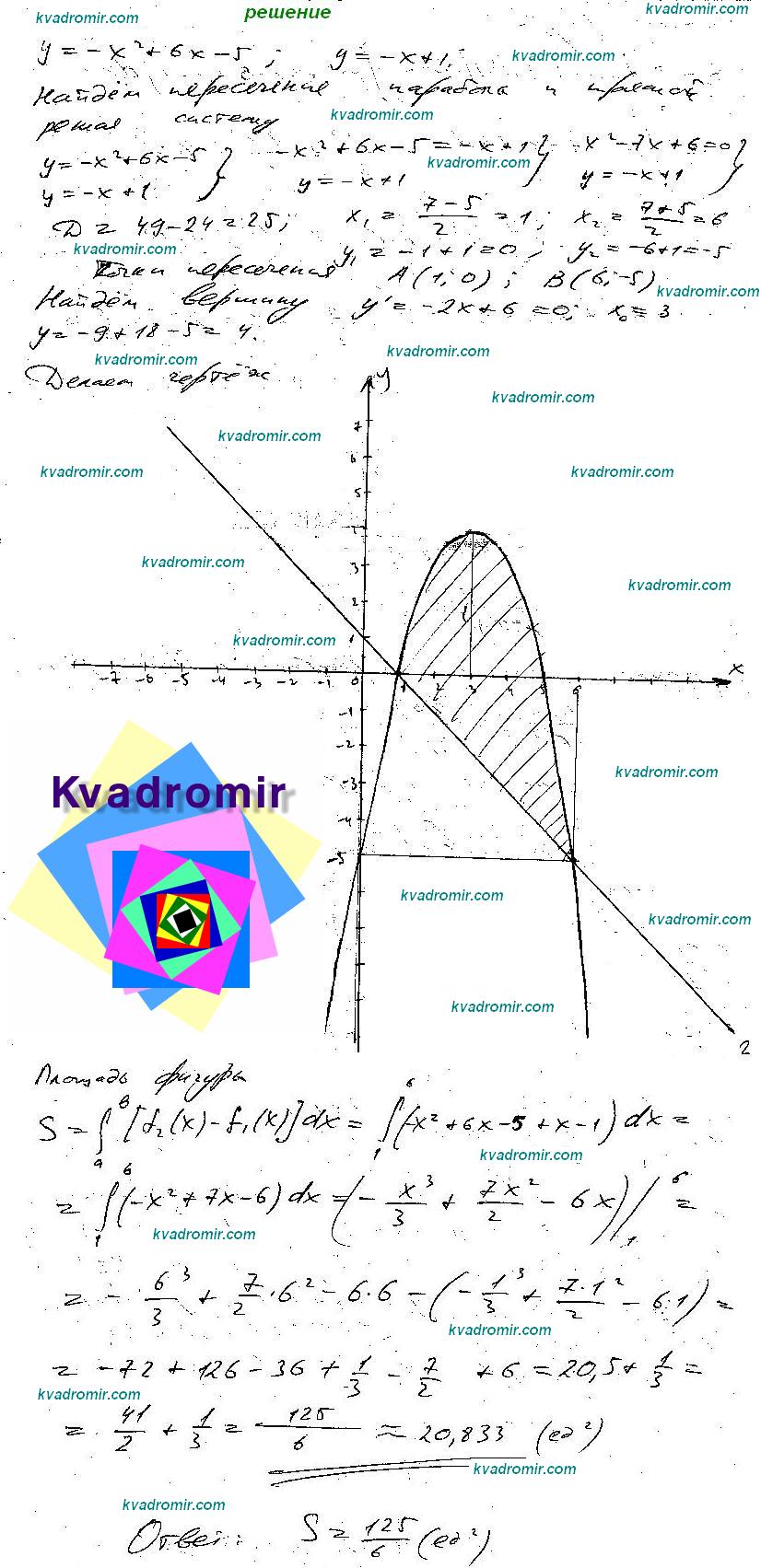
Площадь фигуры
Найти площадь фигуры, ограниченной линиями
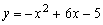 и и 
Решение
 ______________________________________________________________________
______________________________________________________________________
Задача 3557 из Бермана
Решение
 ______________________________________________________________________
______________________________________________________________________
Посмотреть другие совершенно бесплатные решения
Посмотреть другие совершенно бесплатные решения
Решение задач по физике и математике на заказ
Алгебра и аналитическая геометрия
Решение задач по алгебре и геометрии предполагает изучение теоретического материала по следующим темам:
Скалярные и векторные физические величины. Сила, перемещение, скорость, угловая скорость, момент. Вектор как направленный отрезок прямой. Коллинеарные и компланарные векторы. Нулевой вектор. Длина вектора. Равенство векторов. Элементарные операции над векторами: сложение векторов и умножение вектора на число. Свойства элементарных операций над векторами. Векторное пространство.
Линейная комбинация векторов. Линейно зависимые и линейно независимые системы векторов. Базис на прямой, базис на плоскости и базис в пространстве. Разложение вектора по базису. Координаты вектора.
Ортонормированный базис. Декартова прямоугольная система координат. Радиус вектор. Координаты точки. Столбец координат. Изоморфизм пространства радиус-векторов и векторов-столбцов их координат. Векторы размерности n. Арифметическое пространство.
Скалярное произведение векторов Задачи по геометрии на свойства скалярного произведения. Проекция вектора. Выражение скалярного произведения через координаты векторов.
Правая и левая тройки векторов. Векторное произведение векторов Свойства векторного произведения. Площадь параллелограмма.
Смешанное произведение векторов Свойства смешанного произведения векторов. Объем параллелепипеда. Двойное векторное произведение.
Определитель второго и третьего порядков. Правило Саррюса. Свойства определителей. Выражение векторного произведения через координаты сомножителей. Выражение смешанного произведения через координаты сомножителей.
Уравнение прямой на плоскости и в пространстве. Уравнение плоскости в пространстве. Расстояние от точки до плоскости. Взаимное расположение прямых и плоскостей.
Необходимо решить задачу по алгебре с использованием системы линейных уравнений. Правило Крамера.
Матрицы, линейное пространство матриц порядка m?n. Квадратные матрицы. Нулевая и единичная матрицы. Перемножение матриц.
Миноры и алгебраические дополнения. Определители n-го порядка. Вычисление определителя разложением по строке (столбцу). Ранг матрицы.
Невырожденная квадратная матрица. Понятие обратной матрицы. Вычисление обратной матрицы. Матричная запись системы линейных уравнений. Матричная запись решения системы n уравнений с n неизвестными.
Система m линейных уравнений с n неизвестными. Метод Гаусса. Теорема Кронекера-Капелли о существовании решения системы n уравнений с m неизвестными. Система линейных уравнений. Пространство решений. Размерность пространства решений. Общее решение однородной системы линейных уравнений.
Неоднородная система линейных уравнений. Общее решение неоднородной системы линейных уравнений.
Линейный оператор над векторным пространством и его матрица. Собственные векторы и собственные значения линейных операторов.
Преобразование поворота декартовой прямоугольной системы координат. Понятие вектора как инвариантного объекта.
Мнимая единица.Комплексные числа. Решение квадратных уравнений. Комплексные числа как пространство пар действительных чисел и как двумерное векторное пространство. Изображение комплексных чисел и линейные действия с ними. Модуль и аргумент комплексного числа. Тригонометрическая форма записи.
Перемножение комплексных чисел. Формулы Эйлера. Показательная форма комплексного числа. Деление комплексных чисел, извлечение корней. Действительное подпространство комплексных чисел.
Многочлен. Корень многочлена. Теорема Безу. Наличие действительного корня у многочлена с действительными коэффициентами нечетной степени. Сопряженные комплексные корни и разложение на линейные и квадратичные множители. Основная теорема алгебры.
Деление многочленов. Дробная рациональная функция. Правильные и неправильные дроби. Выделение целой части из неправильной дроби. Простейшие дроби. Разложение дробной рациональной функции на простейшие дроби.
Эллипс, гипербола, парабола. Определение и геометрические свойства. Канонические и параметрические уравнения этих кривых. Траектории планет.
Поверхность вращения. Цилиндрические и конические поверхности. Канонические уравнения поверхностей второго порядка – сферы, эллипсоида, гиперболоидов, параболоидов, седловая точка. Конусы и цилиндры.
Полярная система координат на плоскости. Связь между координатами точки в полярной и декартовой системе координат.
Цилиндрическая и сферическая система координат в пространстве. Формулы связи между координатами.
Чтобы решить задачи необходимо иметь навыки по следующим темам:
- Векторы. Длина вектора. Координаты вектора. Направляющие косинусы. Сложение векторов и умножение вектора на число. Коллинеарные и компланарные векторы. Орт вектора.
-
Линейная комбинация векторов. Линейно зависимые и линейно независимые системы векторов. Разложение вектора по базису.
-
Линейное пространство. Базис и размерность линейного пространства.
-
Определители второго и третьего порядков. Правило Саррюса. Свойства определителей.
-
Скалярное произведение векторов. Векторное произведение векторов. Вычисление площади параллелограмма. Условие коллинеарности. Смешанное произведение векторов. Вычисление объёма параллелепипеда. Условие компланарности векторов.
-
Уравнение прямой на плоскости.
-
Уравнение плоскости и прямой в пространстве. Расстояние от точки до плоскости. Взаимное расположение прямых и плоскостей.
-
Система линейных уравнений. Правило Крамера.
-
Матрицы. Действия над матрицами. Умножение матриц. Транспонирование матриц. Ранг матрицы. Способы отыскания ранга матрицы.
-
Миноры и алгебраические дополнения. Определители n-го порядка. Вычисление определителя разложением по строке (столбцу).
-
Обратная матрица. Матричные уравнения. Решение систем линейных уравнений матричным методом.
-
Условие совместности системы. Теорема Кронекера-Капелли. Решение системы линейных уравнений методом Гаусса.
-
Общее решение однородной системы n уравнений с m неизвестными. Общее решение неоднородной системы n уравнений с m неизвестными.
-
Линейный оператор и его матрица в данном базисе. Собственные векторы линейного оператора.
-
Комплексные числа. Действия над комплексными числами. Решение квадратных уравнений. Модуль и аргумент комплексного числа. Тригонометрическая и показательная формы записи. Формулы Эйлера. Показательная форма комплексного числа. Формула Муавра.
-
Многочлен. Корень многочлена. Теорема Безу. Наличие действительного корня у многочлена с действительными коэффициентами нечетной степени. Сопряженные комплексные корни и разложение на линейные и квадратичные множители. Основная теорема алгебры.
Вопросы к экзамену по математике в III семестре
- Числовой ряд.
- Сходимость и сумма ряда.
- Необходимое условие сходимости ряда.
- Гармонический ряд.
- Достаточные признаки сходимости рядов.
- Признаки сравнения рядов.
- Признаки ДАламбера, радикальный и интегральный признаки Коши.
- Знакопеременные и знакочередующиеся ряды.
- Абсолютная и условная сходимость.
- Достаточный признак сходимости знакопеременного ряда.
- Теорема Лейбница.
- Степенные ряды
- Функциональный ряд.
- Область сходимости.
- Равномерная сходимость.
- Степенной ряд. Теорема Абеля.
- Ряды Тейлора и Маклорена.
- Биноминальный ряд.
- Разложение некоторых элементарных функций в ряд Маклорена.
- Применение рядов в приближённых вычислениях.
- Комплексные числа и действия над ними.
- Геометрическая интерпретация комплексного числа.
- Формула Эйлера.
- Алгебраическая форма комплексного числа.
- Тригонометрическая и показательная формы комплексного числа.
- Формула Муавра.
- Расширенная комплексная плоскость.
- Множества точек на плоскость.
- Функция комплексного переменного.
- Действительная и мнимая части функции комплексного переменного.
- Ряды с комплексными членами.
- Представление функций при помощи рядов.
- Показательная и логарифмическая функции.
- Обратные тригонометрические и обратные гиперболические функции.
- Предел и непрерывность функции комплексного переменного.
- Дифференцируемость функции комплексного переменного.
- Производная.
- Необходимое и достаточное условия дифференцируемости.
- Первообразная и неопределённый интеграл.
- Интеграл от функции комплексного переменного по дуге.
- Теорема Коши для односвязной области.
- Теорема Коши для многосвязной области.
- Интегральная формула Коши.
- Ряд Лорана.
- Кольцо сходимости.
- Свойства ряда Лорана.
- Изолированные особые точки.
- Разложение функции в ряд Лорана в окрестности изолированной особой точки.
- Вычет функции.
- Теорема о вычетах.
- Вычисление вычетов.
- Применение вычетов к вычислению интегралов.
- Логарифмический вычет.
- Принцип аргумента.
- Теорема Руше.
- Основная теорема алгебры.
- Преобразование Лапласа и его свойства.
- Оригинал и изображение.
- Дифференцирование и интегрирование изображения.
- Функция Хевисайда.
- Теорема смещения.
- Теорема запаздывания.
- Теорема подобия.
- Свёртка функций.
- Изображение основных элементарных функций.
- Решение дифференциальных уравнений и систем операционным методом.
- Тригонометрический ряд Фурье для функции с периодом 2пи.
- Тригонометрический ряд Фурье для функций с периодом 2l.
- Тригонометрический ряд Фурье для чётной и нечётной функций.
- Разложение непериодической функции в ряд Фурье.
- Ряд Фурье в комплексной форме.
- Ряд Фурье по произвольной ортогональной системе функций.
- Интеграл Фурье.
- Преобразования Фурье.
- Интеграл Фурье в комплексной форме.
- Множества
- Основные операции над множествами.
- Отношения и функции.
- Мощность множества.
- Конечные и бесконечные множества.
- Бинарные отношения.
- Матрица бинарного отношения.
- Отношение эквивалентности.
- Отношение порядка.
- Натуральные числа.
- Принцип математической индукции.
- Системы счисления.
- Элементы теории графов.
- Ориентированные и неориентированные графы.
- Матрицы, порождаемые графом.
- Матрица смежности.
- Матрица инцидентности.
- Эйлеровы и гамильтоновы графы.
- Некоторые задачи теории графов.
- Алгебра логики.
- Логика высказываний. Алгебра логики.
- Формулы алгебры логики.
- Высказывания.
- Отрицание. Конъюнкция. Дизъюнкция. Импликация. Эквивалентность.
- Функции алгебры логики.
- Эквивалентность формул.
- Дизъюнктивные и конъюнктивные нормальные формы.
- Совершенные нормальные формы.
- Минимизация булевых функций.
- Карты Карно.
- Полные системы булевых функций.
Вопросы по предмету Высшая математика
1. Множества: способы задания и основные определения.
2. Операции объединения и пересечения множеств.
3. Операции абсолютного и относительного дополнения и симметрической разности множеств.
4. Декартово произведение множеств. Проекции и свойства декартова произведения.
5. Свойства операций над множествами.
6. Бинарные отношения: способы задания и основные определения.
7. Композиция бинарных отношений и её свойства.
8. Функции (отображения) – основные понятия.
9. Свойства бинарных отношений. Эквивалентность и упорядоченность.
10. Элементарные функции алгебры логики. Эквивалентность функций.
11. Понятие формулы алгебры логики. Вычисление формул. Эквивалентность формул.
12. Свойства элементарных ФАЛ. Эквивалентные преобразования формул.
13. Двойственные функции. Примеры двойственных функций.
14. Принцип двойственности и его применение.
15. Совершенные дизъюнктивные и конъюнктивные нормальные формы – определение и способы построения.
16. Совершенные полиномиальные нормальные формы – определение и способы построения.
17. Полные системы ФАЛ: определение и примеры.
18. Важнейшие замкнутые классы ФАЛ.
19. Теорема Поста о полноте. Следствия. Понятие базиса.
20. Графы – основные определения. Теоремы о степенях вершин графов.
21. Операции над графами.
22. Связность и цикломатическое число графа, свойства связных графов.
23. Оценка числа ребер и критерий связности простого графа.
24. Специальные графы.
25. Планарные графы. Теорема Эйлера о плоских графах.
26. Следствия из теоремы Эйлера о плоских графах.
1.1.Найти среди функций f? и f? несамодвойственную и по лемме S (о несамодвойственной функции) выразить всеми возможными способами все константы.
f?=0001 0111 f?=0001 1001
1.2. Найти среди функций f? и f? немонотонную и по лемме М (о немонотонной функции) выразить всеми возможными способами .
f?=0111 1101 f?=0001 1111
1.3. Найти среди функций f? и f? нелинейную и по лемме L(о нелинейной функции) выразить всеми возможными способами конъюнкцию и дизъюнкцию.
f?=0011 1100 f?=1011 0010
1.4.Проверить полноту системы функций .
f?=1001 0110 f?=0000 0101
1.5.Доказать полноту системы функций . Представить формулами над функции 0,1, ?,&, .
f?=1110 0101 f?=0110 0110
1.6. Доказать полноту системы , состоящую из функции f. Представить формулами над функции 0,1, ?,&, .
f=1110 1100
----------------------------------------------------------
II. Ввести необходимые элементарные высказывания и записать
логической формулой следующее предложение.
“Если идёт дождь или дует сильный ветер, то погода не
подходит для прогулки”.
найти методом преобразования
минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ
построить релейно-контактную схему.
IV. Орграф задан своей матрицей смежности. Следует:
а) нарисовать орграф;
б) найти полустепени и степени вершин;
в) записать матрицу инцидентности.
----------------------------------------------------------
2.1. Найти остов минимальной длины графа G, в котором длины ребер равны соответствующим элементам матрицы A.
2.2.Найти кратчайший путь от вершины до вершины в графе G из задачи 3.1, в котором длины ребер равны соответствующим элементам матрицы A.
2.3.Решить задачу об оптимальном назначении с матрицей эффективности А.
2.4. Найти максимальный поток в транспортной сети, заданной графом , в котором пропускные способности дуг равны соответствующим элементам матрицы A.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра высшей математики
ПРОГРАММА ПО ВЫСШЕЙ МАТЕМАТИКЕ
для студентов 1 курса заочного отделения, все специальности
А. Название разделов.
1. Векторная алгебра и аналитическая геометрия.
2. Элементы линейной алгебры.
3. Введение в математический анализ (теория пределов, непрерывность функций).
4. Дифференциальное исчисление функций одной переменной.
5. Исследование функций и построение графиков с помощью производных.
6. Интегральное исчисление.
Б. Контролирующие мероприятия.
Расчетно-графических работ (в дальнейшем - РГР) - 4.
Контрольных работ (в дальнейшем - КР) - 4.
Экзамен - 2.
Название темы:
1. РГР – 1, часть 1 «Векторная алгебра и аналитическая геометрия».
2. РГР – 1, часть 2 «Линейная алгебра».
3. РГР – 2 «Теория пределов, непрерывность функций».
4. РГР – 3, часть 1 « Техника дифференцирования».
5. РГР – 3, часть 2 «Исследование функций и построение графиков».
6. РГР – 4 «Неопределенный и определенный интегралы ».
7. КР – 1 «Векторная алгебра и аналитическая геометрия » .
8. КР – 2 «Пределы».
9. КР – 3 «Производные».
10. КР – 4 «Неопределенный интеграл».
Экзамен в 1-ом семестре проводится по разделам 1 - 3.
Экзамен во 2-ом семестре проводится по разделам 4 - 6.
В. Содержание занятий.
Введение. Предмет математики и происхождение основных математических понятий. Роль математики в настоящее время, достижения отечественной математической школы.
Векторная алгебра. Определители 2-го и 3-го порядка. Основные свойства (замена строк столбцами, перестановка строк, условие равенства нулю, разложение по элементам строк или столбцов). Индуктивное определение определителя любого порядка на основе разложения по элементам ряда. Скалярные и векторные величины. Вектор как направленный отрезок. Модуль вектора. Равенство векторов, понятие свободного вектора. Коллинеарные и компланарные векторы. Угол между векторами. Линейные операции над векторами и их свойства. Признак коллинеарности двух векторов. Проекция вектора на ось и ее свойства. Базис на плоскости и в пространстве. Разложение вектора по базису, Координаты вектора. Прямоугольные координаты. Линейные операции над векторами, заданными в координатной форме. Скалярное произведение векторов, его свойства, физический смысл. Скалярное произведение в координатной форме. Ориентированные тройки векторов. Векторное произведение векторов, его геометрический и физический смысл. Свойства. Векторное произведение в координатной форме. Смешанное произведение трех векторов, его свойства, геометрический смысл. Вычисление смешанного произведения векторов, заданных в координатной форме.
Аналитическая геометрия. Основная идея аналитической геометрии. Метод координат. Геометрический смысл уравнения F(x,y)=0 на плоскости. Различные способы задания прямой на плоскости и виды уравнений. Исследование общего уравнения прямой. Условия параллельности и перпендикулярности прямых. Кривые второго порядка (окружность, эллипс, гипербола, парабола). Полярные координаты. Геометрический смысл уравнения F(x,y,z)=0. Плоскость. Уравнение плоскости по точке и нормали. Общее уравнение плоскости. Исследование общего уравнения. Условия параллельности и перпендикулярности плоскостей. Задание линии в пространстве пересечением двух поверхностей. Прямая в пространстве как линия пересечения двух плоскостей. Векторное уравнение прямой по точке и направляющему вектору. Параметрические и канонические уравнения прямой. Взаимное расположение прямых к пространстве. Взаимное расположение прямой и плоскости.
Линейная алгебра. n –мерные векторы, линейные операции над ними. Линейная комбинация. Линейная зависимость и линейная независимость векторов в Rn (подробный разбор линейной зависимости в R2 и R3 ) . Понятие линейного пространства и базиса в Rn . Примеры. Линейные операторы и матрицы. Виды матриц (нулевая и единичная). Сложение, умножение на число, произведение (суперпозиция) линейных операторов и соответствующих матриц. Обратный оператор и обратная матрица. Матричная запись системы линейных уравнений. Решение систем линейных уравнений по правилу Крамера и с помощью обратной матрицы. Ранг матрицы. Преобразования, не изменяющие ранга. Теорема о ранге. Следствия. Теорема Кронекера-Капелли. Однородные системы. Решение систем линейных уравнений методом Гаусса.
Введение в математический анализ. Понятие функции одной переменной. Область определения, область значений. Способы задания функций. График функции. Функции, ограниченные в интервале. Сложные функции. Простейшие элементы поведения функций: нули функции, четность и нечетность, возрастание и убывание, периодичность. Основные элементарные функции, их свойства, графики. Определение предела функции при х х0. Графическая иллюстрация понятия предела при х . Предел последовательности. Бесконечно малые функции и их свойства. Бесконечно большие функции и их связь с бесконечно малыми. Теорема о разности между функцией и ее пределом. Теоремы о пределах. Признаки существования пределов (без доказательства). Первый и второй замечательные пределы. Натуральные логарифмы. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые, их свойства. Таблица основных эквивалентных бесконечно малых. Использование эквивалентных бесконечно малых при вычислении пределов. односторонние пределы. Различные определения непрерывности функции в точке, их равносильность. Точки разрыва функции и их классификация. Действия над непрерывными функциями. Непрерывность основных элементарных функций. Непрерывность сложной функции. Непрерывность функции на интервале. Свойства функций, непрерывных на замкнутом интервале.
Дифференциальное исчисление функций одной переменной. Задачи, приводящие к понятию производной. Определение производной , ее геометрический и физический смысл. Уравнения касательной и нормали к кривой. Теоремы о производных суммы, произведения и частного двух функций. Таблица производных основных элементарных функций. Производная сложной функции. Обратная функция и ее производная. Параметрическое задание функции. Производная функции, заданной параметрически. Неявная функция. Производная неявной функции. Производные высших порядков. Механический смысл второй производной. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала. Дифференциал длины дуги плоской кривой. Теоремы Ферма, Ролля, Лагранжа, их геометрический смысл. Теорема Коши. Правило Лопиталя. Формула Тейлора с остаточным членом в форме Лагранжа. Примеры представления некоторых элементарных функций с помощью формулы Тейлора.
Исследование функций и построение графиков с помощью производных. Возрастание и убывание функции на интервале, достаточный признак. Точки экстремума. Необходимый признак. Первый и второй достаточные признаки экстремума. Отыскание наименьшего и наибольшего значений непрерывной на отрезке функции . Выпуклость графика функции вверх и вниз, достаточный признак. Точки перегиба кривой. Необходимый и достаточный признаки. Асимптоты графика функции. Общая схема исследования функции.
Неопределенный интеграл. Первообразная функция. Теорема о разности первообразных. Неопределенный интеграл. Таблица основных интегралов. Простейшие свойства неопределенных интегралов (линейность, инвариантность формул интегрирования). Методы интегрирования: непосредственное интегрирование, замена переменной (включая тригонометрические подстановки), интегрирование по частям. Интегрирование рациональных дробей. Рационализация.
Определенный интеграл и его применение. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральных сумм. Теорема существования определенного интеграла. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Теорема об оценке определенного интеграла, геометрический смысл. Среднее значение функции на отрезке. Теорема о среднем значении, геометрический смысл. Теорема Барроу. Применение определенного интеграла к вычислению площадей плоских фигур (в декартовых, полярных координатах и при параметрическом задании ). Применение определенного интеграла при вычислении объемов тел с известными площадями поперечных сечений , объемов тел вращения, длин дуг плоских кривых и площадей поверхностей вращения. Несобственные интегралы. Признаки сходимости.
Список литературы.
Основная.
1. Привалов И.И. Аналитическая геометрия. М., Наука, 1966 (и последующие издания).
2. Ефимов Н.В. Краткий курс аналитической геометрии. М., Наука, 1975 (и последующие издания).
3. Клетеник Д.В. Сборник задач по аналитической геометрии. М., Наука, 1966 (и последующие издания).
4. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М., Наука, 1969 (и последующие издания).
5. Берман Г.Н. Сборник задач по курсу математического анализа. М., Наука, 1969 (и последующие издания).
Дополнительная.
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. М., Наука. 1977 (и последующие издания).
2. Бугров Н.С., Никольский С.М., Дифференциальное и интегральное исчисление. М., Наука. 1980 (и последующие издания).
3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., Наука, 1976 (и последующие издания).
4. Самохин М.В., Каган М.Л. Математика в инженерном вузе. Алгебра и геометрия. М., Стройиздат, 2003г.
5. Каган М.Л., Макаров В.И., Петелина В.Д. Алгебра и геометрия в вопросах и задачах. Учебное пособие. МГСУ, 2005г.
6. Пакет методической литературы кафедры высшей математики.
|
|
Любопытные задачи по физике
|





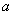 , удовлетворяющего неравенствам
, удовлетворяющего неравенствам 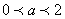 найти наименьшее значение выражения
найти наименьшее значение выражения 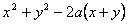 при условии
при условии 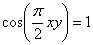 .
.
 ______________________________________________________________________
______________________________________________________________________










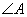 и
и 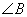 связаны соотношением
связаны соотношением 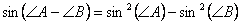

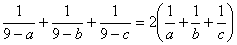 .
Найти площадь треугольника.
.
Найти площадь треугольника.



 ______________________________________________________________________
______________________________________________________________________

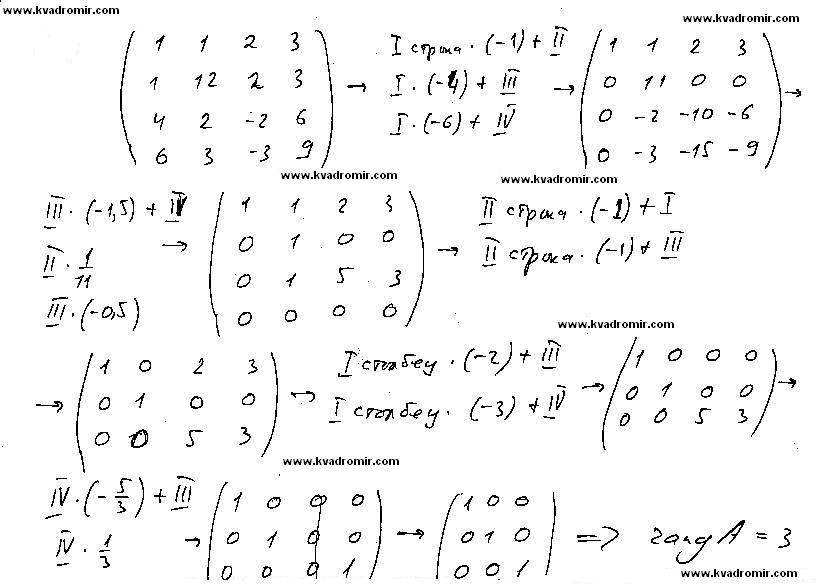
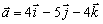 ,
, 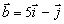 ,
, 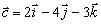
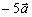 и
и 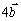 ;
;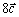 и
и 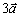 ;
; и
и 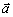 , и являются ли они ортогональными;
, и являются ли они ортогональными;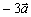 ,
,  ______________________________________________________________________
______________________________________________________________________
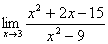
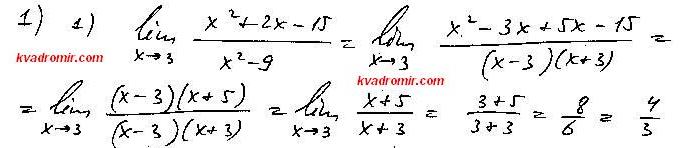 ______________________________________________________________________
______________________________________________________________________
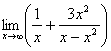
 _________________________________________________________________________________
_________________________________________________________________________________
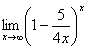
 _________________________________________________________________________________
_________________________________________________________________________________

 _________________________________________________________________________________
_________________________________________________________________________________
 _________________________________________________________________________________
_________________________________________________________________________________
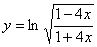


 ______________________________________________________________________
______________________________________________________________________
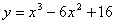
 ______________________________________________________________________
______________________________________________________________________
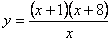
 ______________________________________________________________________
______________________________________________________________________
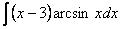
 ______________________________________________________________________
______________________________________________________________________
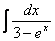
 _________________________________________________________________________________
_________________________________________________________________________________
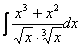
 _________________________________________________________________________________
_________________________________________________________________________________
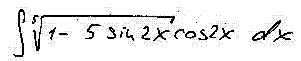
 ______________________________________________________________________
______________________________________________________________________
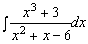
 ______________________________________________________________________
______________________________________________________________________
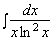
 ______________________________________________________________________
______________________________________________________________________
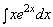
 ______________________________________________________________________
______________________________________________________________________
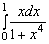
 ______________________________________________________________________
______________________________________________________________________
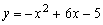 и
и 
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________